1. в прямоугольном параллелепипеде abcda1b1c1d1 угол между прямыми b1d1 и cd1 равен 90 и ab: ad=1: 2. найти угол между прямыми ac и a1d
2. на рёбрах bb1 и c1d1 куба abcda1b1c1d1 взяты соответственно точки p и q такие, что bp: bb1 = 2: 3, c1q: c1d1 = 1: 4. плоскость, проходящая через точки a, p, q пересекает прямые dd1 и b1c1 соответственно в точках e и f. найти угол между прямыми ef и a1c
АВ = CD = 2
Объяснение:
Дано: ABCD - трапеция.
∠А = 60°; ∠С = 120°;
ВС = 3; AD = 5.
Найти: АВ и CD.
ВН - высота.
1. Рассмотрим ABCD.
Углы, прилежащие к боковой стороне трапеции в сумме равны 180°.⇒ ∠В = 180° - 60° = 120°
∠D = 180° - 120° = 60°
Если углы при основаниях трапеции равны, то трапеция - равнобедренная.⇒ АВ = CD
2. Рассмотрим ΔАВН - прямоугольный.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшее из которых равна полуразности оснований.⇒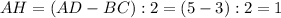
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠1 = 90° - 60° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ AB = AН ·2 = 1 · 2 = 2
АВ = CD = 2
При перетині прямих утворюються 2 пари суміжних кутів. Оскільки сума суміжних кутів дорівнює 180°, то сума двох пар дорівнюватиме 180°×2=360°. Один з кутів дорівнює 360°-280°=80°. При перетині двох прямих утворюються 2 пари вертикальних кутів, що лежать навпроти один одного. Оскільки один з кутів дорівнює 80°, то вертикальний кут, що знаходиться у парі з ним, теж дорівнює 80°. Сума двох інших вертикальних кутів дорівнює 280°-80°=200°. Щоб знайти один з ціх кутів, треба їхню суму поділити на два, бо ці кути рівні. Маємо: 200°÷2=100°. Тож два інші вертикальні кути дорівнюють по 100°.
Відповідь: кути дорівнюють 80°, 100°, 80°, 100°.