1. В прямоугольном треугольнике АВС ( угол С = 90о) АС = 3 см, ВС= √3. Найдите угол В и гипотенузу АВ.
2. В треугольнике АВС средняя линия МК параллельна АС и равна
13,6 см. Найдите длину стороны АС.
3. В прямоугольном треугольнике АВС ( угол С= 90о) катеты ВС = 20 см, АС = 15 см. Найдите синус, косинус и тангенс угла А.
4. Средние линии треугольника относятся как 1:3:4, а периметр треугольника равен 48 см. Найдите стороны треугольника.
Відповідь:
1)Гипотенуза АВ=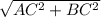 =
=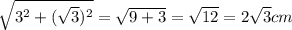
cos∠B=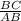 ; cos∠B=
; cos∠B=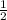 ; ∠B=60°
; ∠B=60°
2)Средняя линия треугольника равна половине длины параллельной стороны
МК=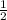 АС
АС
АС=27,2см
3)AB=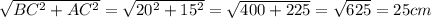
sin∠A=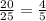
cos∠A=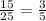
tg∠A=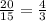
4)Средние линии относятся как 1:3:4, а средняя линия треугольника равна половине длины параллельной стороны, тогда стороны будут относиться как 2:6:8 и их можно записать как 2х, 6х, 8х
Р=48см
Р=2х+6х+8х
2х+6х+8х=28
16х=48
х=3
2х→6см
6х→18см
8х→24см
Стороны треугольника имеют величины 6см, 18см, 24см