1)В прямоугольном треугольнике (∠B = 90°) величина угла A составляет 60°. Из вершины угла A проведена биссектриса AD, которая разбивает противоположный катет на отрезки BD и DC. 1. Докажите, что ΔBCA∼ΔBAD.
2. Найдите отношение BD:DС. ответ запишите в виде отношения чисел.
2)В треугольнике ABC проведена средняя линия NM (NM || AC). В полученном треугольнике BNM проведена средняя линия PF (PF || BN). Определите периметр треугольника PMF, если периметр треугольника ABC составляет 120 см.
Треугольник АВС
Высота ВН делит его на два прямоугольных треугольника АВН и СВН, где АВ и ВС - гипотенузы.
Примем АН за х.
Тогда СН = АС-х
Составляем два уравнения:
Для треугольника АВН:
ВН^2 = АВ^2 - х^2
Для треугольника СВН:
ВН^2 = ВС^2 - (АС -х)^2
Так как левые части этих уравнений равны, то равны и правые.
АВ^2 - х^2 = ВС^2 - (АС -х)^2
АВ^2 - х^2 - ВС^2 + АС^2 -2АС•х + х^2 = 0
2х•АС = АВ^2 - ВС^2 + АС^2
х = (АВ^2 - ВС^2 + АС^2) / 2АС
Тогда значение х можно вставить в уравнение:
ВН^2 = АВ^2 - х^2
ВЕ^2 = АВ^2 - ((АВ^2 - ВС^2 + АС^2) / 2АС)^2
Объяснение:
Объяснение:
Дано: ABCD - параллелограмм.
AE = ED; DF = FC.
BE ∩ AC = G; BF ∩ AC = H;
S (ABCD) = 12.
Найти: S (GHFE)
1. Рассмотрим ΔABD и ΔDBC.
Любая диагональ параллелограмма делит его на два равных треугольника.⇒ S (ΔABD) = S (ΔDBC) = 12:2 = 6
Аналогично:
S (ΔABC) = S (ΔACD) = 12:2 = 6
2. Рассмотрим ΔABD.
AE = ED (условие) ⇒ВЕ - медиана.
Медиана делит треугольник на два равновеликих треугольника.⇒ S (ΔABE) = S (ΔEBD) = 6:2 = 3
3. Рассмотрим ΔDBC.
DF = FC ⇒ BF - медиана.
S (ΔDBF) = S(ΔFBC) = 6:2 = 3
4. Рассмотрим ΔACD.
AE = ED; DF = FC (условие)
⇒ EF - средняя линия.
Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвертой площади исходного треугольника.⇒
5. Найдем площадь ΔEBF.
S (ΔEBF) = S (ABCD) - S(ΔABE) - S(ΔFBC) - S(ΔEFD) =
6. Рассмотрим ΔABD.
BF - медиана (п.3)
Диагонали параллелограмма точкой пересечения делятся пополам.⇒ BO = OD ⇒ СО - медиана.
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.⇒ BH : HF = 2:1
или ВН : BF = 2:3
7. Рассмотрим ΔABD.
Аналогично п.6: BE и AO - медианы.
⇒BG : GE = 2 :1
или BG :BE = 2:3
8. Рассмотрим ΔGBH и ΔEBF.
∠B - общий. ВН : BF = 2:3 (п.6); BG :BE = 2:3 (п.7)
⇒ ΔGBH ~ ΔEBF, k =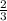
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.Найдем площадь GHFE: