1.В равнобедренном треугольнике ABC проведена высота - вопрос №11211797780 от goodanonim 13.10.2022 16:46

Question

Геометрия: 1.В равнобедренном треугольнике ABC проведена высота BD к основанию AC. Длина высоты — 12,3 см, длина боковой стороны — 24,6 см. Определи углы этого треугольника. ∡ BAC = °; ∡ BCA = °; ∡ ABC = °. 2.Высоты треугольника пересекаются в точке O. Величина угла ∡ BAC = 88°, величина угла ∡ ABC = 67°. Определи угол ∡ AOB. ∡ AOB = °. 3. В треугольнике OPM проведена высота PD. Известно, что ∡ POM = 31° и ∡ OPM = 115°. Определи углы треугольника DPM. ∡ PDM = °; ∡ DPM = °; ∡ PMD = °. 4.В равнобедренном треугольнике

goodanonim · Answer

Для любой правильной призмы справедливы формулы:

Площадь боковой поверхности:

Sбок = Pосн · h, где

Росн - периметр основания,

h - высота.

Площадь полной поверхности:

Sполн = Sбок + 2Sосн

Объем:

V = Sосн · h

____________________

a - сторона основания.

____________________

Правильная треугольная призма:

в основании лежит правильный треугольник, значит

Sосн =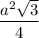 $\dfrac{a^{2}\sqrt{3}}{4}$

Sбок = 3а · h

Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2

$V=\dfrac{a^{2}\sqrt{3}}{4}\cdot h$

____________________

Правильная четырехугольная призма:

в основании - квадрат, значит

Sосн = a²

Sбок = 4ah

Sполн = 4ah + 2a²

V = a²h

____________________

Правильная шестиугольная призма:

Sосн =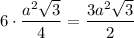 $6\cdot \dfrac{a^{2}\sqrt{3}}{4}=\dfrac{3a^{2}\sqrt{3}}{2}$

Sбок = 6ah

Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3

$V=\dfrac{3a^{2}\sqrt{3}}{2}\cdot h$