1. В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 49. Найдите площадь четырёхугольника ABMN.

2.Какие из следующих утверждений верны?
(Укажи несколько правильных вариантов ответа)

А. Через любые три точки проходит не более одной прямой.
Б. Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 83° и 97° , то эти две прямые параллельны.
В. Если угол равен 70° , то смежный с ним равен 110° .
Г. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 140° , то эти две прямые параллельны.

Показать ответ

Ответ:

Макс00796

20.06.2022 14:59

1. Верно ли утверждение: "Четырехугольник является правильным, если все его углы равны между собой"?

б) нет, так как должны быть равны и стороны, иначе это может быть прямоугольник.

2. Все стороны многоугольника являются хордами окружности. Можно ли утверждать, что многоугольник описан около окружности?

б) нет, этот многоугольник вписан в окружность.

3. Чему равна дуга окружности (в градусах), стягиваемая стороной правильного треугольника?

б) 120° (360° : 3) .

4. Сколько сторон имеет правильный многоугольник, у которого сумма всех его углов равна 540°?

Сумма углов многоугольника равна 180°(n - 2), где n - количество сторон.

180°(n - 2) = 540°

n - 2 = 3

n = 5

а) 5.

5. Чему равна длина окружности, если ее диаметр равен 50 см?

С = πd = 50π см

а) 50π см.

6. Из круга, радиус которого равен 20 см, вырезан сектор. Дуга сектора равна 90°. Чему равна площадь оставшейся части круга?

Дуга оставшейся части круга:

α = 360° - 90° = 270°

Sсект = πR² · α / 360°

Sсект = π · 400 · 270° / 360° = 300π см²

а) 300π см²

0,0(0 оценок)

Ответ:

диван111111

14.09.2021 10:21

а)

Сейчас поэкспериментируем!

Формула вычисления суммы углов многоугольника такова: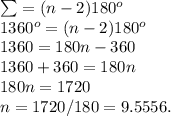 $\sum = (n-2)180^o\\1360^o = (n-2)180^o\\1360 = 180n-360\\1360+360 = 180n\\180n = 1720\\n = 1720/180 = 9.5556.$

Как мы видим — число не целое, что и означает, что правильный многоугольник, чъя сумма углов равна 1360° — не сущестувет.

б)

Фромула вычисления внуреннего угла в правильном многоуольнике такова:

$\displaystyle\\x = \sum_\angle/n\\160^o = \sum_\angle/n\\\\\\\left \{ {{160^0 = \sum/n} \atop {\sum = (n-2)180^o}} \right. \\\sum = 160n\\160n = (n-2)180^o\\160n = 180n-360^o\\20n = 360^o\\n = 360/20 = 18.$

Количество углов — 18, сумма углов: (18-2)180 = 2880°, каждый внутренний угол равен: 160°.

Да, такой многоугольник может существовать.

в)

Нет, наоборот: радиус описанной окружности больше радиуса вписанной окружности.

Например есть теорема, что радиус описанной окружности около правильного треугольника — в 2 раза больше радиуса вписанной окружности в этот же треугольник.

Один из концов радиуса описанной окружности — не лежит на нём, и не находится в мноугольнике, в то время как радиус вписанной окружности — можно провести через вершины многоугольника до центра окружности.

0,0(0 оценок)

Популярные вопросы: Геометрия