если внутренние накрест лежащие углы равны, то прямые параллельны.
если соответственные углы равны, то прямые параллельны.если сумма внутренних односторонних углов равна 180, то прямые параллельны.следствие: две прямые, перпендикулярные третьей, параллельны. свойства параллельных прямых
теорема 2. две прямые, параллельные третьей, параллельны.
это свойство называется транзитивностью параллельности прямых.
теорема 3. через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
теорема 4. если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
на основании этой теоремы легко обосновываются следующие свойства.
если две параллельные прямые пересечены третьей прямой, то соответствующие углы равны.если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180. следствие если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Т.к. О - центр вписанной в ΔАВС окружности, то О - точка пересечения биссектрис углов ΔАВС. Значит, АО и ВО - биссектрисы.
Т.к. О1 - центр внеписанной окружности то О1 - точка пересечения биссектрис внешних углов ΔАВС. Значит, АО1 и ВО1 - биссектрисы.
Пусть α - величина внешнего угла ΔАВС при вершине А, тогда (180°-α) - величина внутреннего угла ΔАВС при вершине А, т.к. эти углы - смежные.
Тогда
Аналогично,
Рассмотрим четырехугольник АОВО1.
У него сумма противолежащих углов А и В равна 90°+90° = 180°.
Т.к. сумма всех углов этого выпуклого четырехугольника равна 360°, то сумма двух других противолежащих при вершинах О и О1 также равна 180°.
Таким образом, воспользуемся утверждением: если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Делаем вывод, точки А, В, О и О1 лежат на одной окружности.
теорема 1. признак параллельности прямых
если внутренние накрест лежащие углы равны, то прямые параллельны.
если соответственные углы равны, то прямые параллельны.если сумма внутренних односторонних углов равна 180, то прямые параллельны.следствие: две прямые, перпендикулярные третьей, параллельны. свойства параллельных прямыхтеорема 2. две прямые, параллельные третьей, параллельны.
это свойство называется транзитивностью параллельности прямых.
теорема 3. через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
теорема 4. если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
на основании этой теоремы легко обосновываются следующие свойства.
если две параллельные прямые пересечены третьей прямой, то соответствующие углы равны.если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180. следствие если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.Чертеж к решению - во вложении.
Т.к. О - центр вписанной в ΔАВС окружности, то О - точка пересечения биссектрис углов ΔАВС. Значит, АО и ВО - биссектрисы.
Т.к. О1 - центр внеписанной окружности то О1 - точка пересечения биссектрис внешних углов ΔАВС. Значит, АО1 и ВО1 - биссектрисы.
Пусть α - величина внешнего угла ΔАВС при вершине А, тогда (180°-α) - величина внутреннего угла ΔАВС при вершине А, т.к. эти углы - смежные.
Тогда
Аналогично,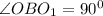
Рассмотрим четырехугольник АОВО1.
У него сумма противолежащих углов А и В равна 90°+90° = 180°.
Т.к. сумма всех углов этого выпуклого четырехугольника равна 360°, то сумма двух других противолежащих при вершинах О и О1 также равна 180°.
Таким образом, воспользуемся утверждением: если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Делаем вывод, точки А, В, О и О1 лежат на одной окружности.
Доказано.