1.вказати правильне твердження.а) площа прямокутного трикутника дорівнює добутку катетів; б) діагоналі ромба рівні; в) медіани трикутника перетинаються в одній точці та поділяються неюу відношенні 2: 1, рахуючи від вершини трикутника; г) sin60° = 1чи можуть кути прямокутної трапеції дорівнювати 35° і 145°? а) так; б) ні; в) не можна визначити.трикутник cbd подібний трикутнику amk. чому дорівнює кут в три-кутника cbd, якщо za = 73°, 2k = 27°? а) 100°; б) 46°; в) 80°; г) 90°.за рисунком знайти кут aod.а) 60°; б) 120°; в) 30°; г) 90°.5 см3 смnmn — середня лінія трапеції abcd. площутрапеції обчислюють так: а) (5 - 8) см”; б) (3-5) см; в) 3+3 см; г) 8+5.3 (см).8 см
Точка одинаково удалена от всех вершин прямоугольного треугольника на 1 см, а от плоскости этого треугольника на 0.5 см найдите медиану гипотезе этого треугольника
Объяснение:
1.Пусть КМ-медиана ΔAКB - равнобедренный, поэтому КM ⊥ AB по свойству медианы равнобедренного треугольника.
Пусть в ΔКCM проведем КO⊥ СМ. Тогда ОА=ОВ=ОС как проекции равных наклонных равный наклонные, поэтому ОА = ОВ= ОС = R, R - радиус описанной окружности около ΔАВС. Но центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы , поэтому точки М и О совпадают. ⇒
КM ⊥ ( АВС).
2)Т.к. М-середина АВ , то СМ-медиана к гипотенузе ΔАВС.
ΔАКМ-прямоугольный, АК=1 см, КМ=0,5 см, по т. Пифагора АМ=√(1²-0,5²)=√0,75=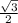
( см).
R=АМ=ВМ=СМ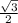, СМ=
см
Объяснение:
1)
∆ADC- прямоугольный.
По теореме Пифагора найдем гипотенузу
АС=√(AD²+DC²)=√(29+25)=√54.
∆ACB- прямоугольный.
По теореме Пифагора найдем гипотенузу
АВ=√(АС²+СВ²)=√(54+36)=√90=3√10
ответ: АВ=3√10
2)
∆АСD- прямоугольный.
По теореме Пифагора найдем катет
АС=√(AD²-CD²)=√(3²-2²)=√(9-4)=√5
∆ABC- прямоугольный.
По теореме Пифагора найдем катет
АВ=√(АС²-ВС²)=√(5-3)=√2
ответ: АВ=√2
3)
∆ADC- прямоугольный.
По теореме Пифагора найдем гипотенузу.
АС=√(АD²+DC²)=√(7²+6²)=√(49+36)=√85
∆ACB- прямоугольный.
По теореме Пифагора найдем гипотенузу
АВ=√(АС²+СВ²)=√(85+15)=√100=10
ответ: АВ=10