1)Знайдіть відстань між точками А і В,якщо :А(2;1;5),В(-4;1;1)
а)8 b)10 c)11 d)9
2)Знайдіть відстань від точки К (3;7;4)до осі ординат.
а)5 b)6 c)7 d)8
3)Точка N належить осі ординат.Відстань від точки N до точки М (-1;5;2)дорівнює 3.Знайдіть координати точки N.
а)(7;0;0) b)(0;7;0) c)(7;0;7) d)(0;7;7)
ОД = Н/tg 60° = 10√3 / √3 = 10.
ОД (по свойству медиан) = (1/3) СД =(1/3)*а*cos 30° = (1/3)*a *(√3/2) = a√3/6. Отсюда а (сторона основания пирамиды) равно: а = 6*ОД/√3 = 6*10/√3 = 60/√3 = 20√3.
Периметр основания Р = 3а = 3*20√3 = 60√3.
Апофема SД = Н/sin 60° = 10√3/(√3/2) = 20 = А.
Площадь боковой поверхности:
Sбок = (1/2)Р*А = (1/2)*60√3*20 = 600√3.
Площадь основания:
Sо = а²√3/4 = (20√3)²*√3/4 = 300√3.
Площадь полной поверхности:
S = Sо + Sбок = 300√3 + 600√3 = 900√3.
Объём пирамиды V = (1/3)Sо*H = (1/3)*(300√3)*(10√3) =
= 3000.
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть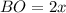
см и 
см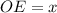, тогда 
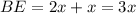, что по условию он равен 9 см.
Следовательно,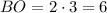
см и 
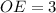см
Аналогично, пусть теперь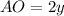
см и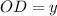 
, тогда 
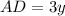и по условию равен 12 см
Таким образом,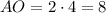
см и 
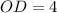см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника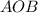
По теореме Пифагора из прямоугольного треугольника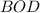
Тогда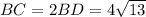
см
Из прямоугольного треугольника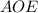
по теореме Пифагора
Тогда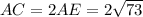
см
ответ:
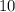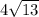см;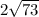 
см; 
см.