1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10
По теореме Пифагора, диагональ = =, где а - сторона квадрата
2) Сумма улов n-угольника s = 180(n - 2)
1600 = 180(n - 2);
1600 = 180n - 360;
1960 = 180n;
196 = 18n;
n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует
3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =
(a - сторона ромба )
По свойству ромба все его стороны равны тогда P ромба = 4a
если провести прямую с точки F в точку D то будет прямоугольный треугольник, и того с этого треугольника найдем ДФ с теоремы пифагора, нам известна сторона АФ = 4 и АД = 4 и ДФ = корень из АФ в квадрате + АД вквадрате = корень из 32
потом проведем източки Ф в точку С и найдем по тойже схеме по теореме пифагора а нам известно что БФ = 8 а БЦ = 4 и того корень кв из 8 в квадрате + 4 в квадрате = корень из 80.
таким образом мы нашли длины прых из точки Ф в точки Ц иД ФЦ = корень из 80, ЦД = корень из 32
1)Диагональ квадрата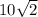
2)Такого правильного многоугольника не существует
3)Периметр ромба 60
Объяснение:
1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10
По теореме Пифагора, диагональ =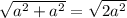
=
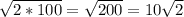, где а - сторона квадрата
2) Сумма улов n-угольника s = 180(n - 2)
1600 = 180(n - 2);
1600 = 180n - 360;
1960 = 180n;
196 = 18n;
n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует
3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =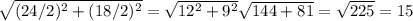
(a - сторона ромба )
По свойству ромба все его стороны равны тогда P ромба = 4a
= 4 * 15 = 60
если провести прямую с точки F в точку D то будет прямоугольный треугольник, и того с этого треугольника найдем ДФ с теоремы пифагора, нам известна сторона АФ = 4 и АД = 4 и ДФ = корень из АФ в квадрате + АД вквадрате = корень из 32
потом проведем източки Ф в точку С и найдем по тойже схеме по теореме пифагора а нам известно что БФ = 8 а БЦ = 4 и того корень кв из 8 в квадрате + 4 в квадрате = корень из 80.
таким образом мы нашли длины прых из точки Ф в точки Ц иД ФЦ = корень из 80, ЦД = корень из 32