100 1)в основе прямоугольной призмы лежит ромб одна из диагоналей которого 126 см, а сторона ромба 105 см найдите объем призмы если ее высота равна 1/242)найти обьем правильной четырехугольной пирамиды ,если высота пирамиды=h,а боковое ребро наклонено к плоскости основания под углом a3)основой пирамиды является ромб со стороной 5 см и углом 135°.двухгранные углы при основании равны и ровняются 45°.найдите площадь боковой поверхности пирамиды

ABCD - квадрат со стороной, равной α, BM ⊥ ABC, BM = α. Найдите двугранный угол, образованный гранями AMD и CMD.

Объяснение:

1) Пусть АР⊥MD,  соединим Р и С.

Т.к. АВ⊥AD, то по т. о трех перпендикулярах МА⊥AD⇒ΔAMD-прямоугольный. Т.к. ВС⊥СD, то по т. о трех перпендикулярах МС⊥CD ⇒ΔCMD-прямоугольный

2) Прямоугольные ΔAMD=ΔCMD по катету ( AD=CD стороны квадрата) и гипотенузе (MD--общая), значит и СР⊥MD, Поэтому ∠АРС-линейный угол двугранного , образованный гранями AMD и CMD.

3 ) Применим т. косинусов для ΔАРС :

АС²=АР²+РС²-2*АР*РС*cos∠APC. Найдем отрезки АС, АР, РС.

4) Из ΔАВС , АС²=2а² , АС=а√2.

Из ΔАВМ , АМ²=2а² , АМ=а√2.

Из ΔАМD , DM²=2а²+a² , DM²=3a²  ,DM=a√3 .

ΔADM подобен ΔPDA  по 2-м углам : ∠D-общий , ∠МАD=∠APD=90°, значит сходственные стороны пропорциональны   ,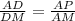

АР=(AD*AM):DM=(а*а√2) :a√3=a* .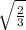

ΔADP=ΔCDP как прямоугольные по катету и гипотенузе⇒РС=a* .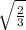

4) "Закидываем " найденные значения в АС²=АР²+РС²-2*АР*РС*cos∠APC.

(а√2)²=2*(a*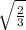 )²-2*(a* 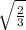) cos∠APC ,

2a²=2a² *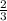 -2a² * 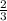*cos∠APC ,

1=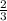   (1 - cos∠APC) ,   cos∠APC= -0,5   ,∠APC=120° .

∆АМС - рівнобедрений

Объяснение:

Доведения:

Нехай дано ∆АВС - рівнобедрений (АВ = ВС), АЕ - медіана,

CF - медіана, АЕ i CF перетинаються в точці М.

Доведемо, що ∆АМС - рівнобедрений.

Розглянемо ∆AFC i ∆СЕА.

1) ∟A = ∟C (∆АВС - рівнобедрений).

2) АС - спільна.

3) AF = 1/2АВ, CF - медіана. СЕ = 1/2ВС, АЕ - медіана.

АВ =ВС (∆АВС - рівнобедрений). AF = СЕ.

Отже, ∆AFC = ∆СЕА за I ознакою piвностi трикутників,

з цього випливає, що ∟EAC = ∟FCA.

Розглянемо ∆АМС.

Оскільки ∟MAC = ∟MCA, то ∆АМС - рівнобедрений