Пусть MABCD - данная правильная пирамида, ее апофема - МЕ.
Проведем высоту МО.
В прямоугольном Δ МЕО ∠ ОМЕ = 90°-60° = 30°.
Значит, катет ОЕ равен половине гипотенузы МЕ: ОЕ=√3.
Т.к. пирамида правильная, то Е - середина DC.
Точка О - середина АС. Значит, ОЕ - средняя линия ΔACD. Тогда ОЕ||AD и AD=2OE =2√3
Значит,
В прямоугольном Δ МЕО по тереме Пифагора МО² = МЕ² - ОЕ²
Таким образом,
ответ: 12.
Пусть MABCD - данная правильная пирамида, ее апофема - МЕ.
Проведем высоту МО.
В прямоугольном Δ МЕО ∠ ОМЕ = 90°-60° = 30°.
Значит, катет ОЕ равен половине гипотенузы МЕ: ОЕ=√3.
Т.к. пирамида правильная, то Е - середина DC.
Точка О - середина АС. Значит, ОЕ - средняя линия ΔACD. Тогда ОЕ||AD и AD=2OE =2√3
Значит,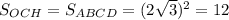
В прямоугольном Δ МЕО по тереме Пифагора МО² = МЕ² - ОЕ²
Таким образом,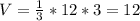
ответ: 12.