Уравнение окружности имеет вид , где и - координаты центра окружности, а - её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае: .
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: .
/_A = 72°, а =12,3 см. с = 12,9 см.
Объяснение:
В прямоугольном треугольнике сумма острых углов равна 90°. Следовательно, ZA = 90° - 18° = 72°.
В треугольниках приняты обозначения:
a,b,c — длины сторон BC,AC и АВ треугольника АВС соответственно.
В прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к гипотенузе. Следовательно,
SinB = b/c => c = b/Sinb = 4/sin18.
Соответственно, катет а найдем ир
соотношения:
SinA = a/c => a = c-SinA = 4.Sin72/Sin18.
Или так:
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему. Следовательно,
tgb = b/a => a = b/tgb = 4/tg18. =
остается найти значения тригонометрических функций соответствующих углов по таблицам или калькулятором.
Sin18 = 0,309. Sin72 = 0,951. Tg18 = 0,325. Тогда
с = 4/sin18 = 4/0,309 = 12,9 см.
a = 4.Sin72/Sin18 = 4-0,951/0,309 = 12,3
см. Или
a = 4/tg18 = 4/0,325 = 12,3 см.
Уравнение окружности имеет вид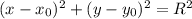 , где
, где 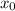 и
и 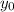 - координаты центра окружности, а
- координаты центра окружности, а 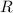 - её радиус.
- её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае: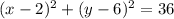 .
.
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: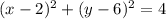 .
.