12**. При симетрії відносно деякої точки К точка м(12; -1)
переходить у точку N(2; -3). Знайти координати точки, в яку при цій
симетрії перейде точка Р1;1).

Если на ребрах  тетраэдра  abcd отмечены точки v (на ребре ab), r (на ребре bd) и t (на ребре cd), а по условию нужно построить сечение  тетраэдра  плоскостью vrt, то постройте, прежде всего, прямую, по которой плоскость vrt будет пересекаться с плоскостью abc. в данном случае точка v будет общей для плоскостей vrt и abc. 2для того чтобы построить еще одну общую точку, продлите отрезки rt и bc до их пересечения в точке k (данная точка и будет второй общей точкой для плоскостей vrt и abc). из этого следует, что плоскости vrt и abc пересекаться будут по прямой vк. 3в свою очередь прямая vк пересечет ребро ас в точке l. таким образом, четырехугольник vrtl и является искомым сечением  тетраэдра, построить которое нужно было по условию . 4обратите внимание на то, что, если прямые rt и bc параллельны, то прямая rt параллельна грани авс, поэтому плоскость vrt пересекает данную грань по прямой vк', которая параллельна прямой rt. а точка l будет точкой пересечения отрезка ас с прямой vк'.  сечениететраэдра  будет все тем же четырехугольником vrtl. 5допустим, известны следующие исходные данные: точка q находится на боковой грани adb  тетраэдра  abcd. требуется построить сечение этого  тетраэдра, которое бы проходило через точку q и было бы параллельным основанию abc. 6ввиду того, что секущая плоскость параллельна основанию abc, она также будет параллельна прямым ав, вс и ас. а значит, секущая плоскость пересекает боковые грани  тетраэдра  abcd по прямым, которые параллельны сторонам треугольника-основания авс. 7проведите из точки q прямую параллельно отрезку ав и обозначьте точки пересечения данной прямой с ребрами ad и bd буквами m и n. 8затем через точку m проведите прямую, которая бы проходила параллельно отрезку ас, и обозначьте точку пересечения данной прямой с ребром cd буквой s. треугольник mns и есть искомым сечением.

1)  Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.

То есть, если точка А лежит на единичной окружности, то её координаты можно записать так:    .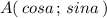

Основное тригонометрическое тождество имеет вид:   .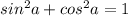

Поэтому проверяем это тождество для заданных координат.

На единичной окружности лежит точка    .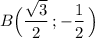

Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.

Смотри рисунок.

Так как  sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .