13. (Б) У многоугольника всего 20 диагоналей. Сколько у него сторон? 14. (Б) Разрежьте пятиконечную звезду на пять выпуклых фигур.
15. (А) Диагональ BD четырехугольника ABCD образует равные углы сего
сторонами AB и CD. Известно, что AB = CD. Докажите, что BC = AD.
16. (Б) В четырёхугольнике ABCD диагональ AC делит углы BAD и BCD пополам,
Докажите, что его диагонали перпендикулярны.
17. (Б) Внутри прямого угла взяли любую точку М. Её отразили симметрично
относительно сторон этого угла и получили точки M, и М. Докажите, что
вершина угла лежит на середине отрезка M, M..
18. (Б) В четырёхугольнике ABCD стороны AB и CD равны. Его диагонали тоже
равны и пересекаются в точке 0. Докажите, что АО = D0.
19. (А) Прямая пересекает две параллельные в точках А и В. Биссектрисы двух
смежных углов с вершиной в точке В при одной из этих прямых пересекают
другую параллельную прямую в точках Си Е. Докажите, что AC = AE.
20. (А) В пятиугольнике ABCDE стороны AB и DE параллельны, а углы ABC и CDE
равны 100° и 120° соответственно. Найдите величину угла BCD.
2
ответ: БИЛЕТ№1
1. отрезок -прямая, которая имеет начало и конец, обозначается с обоих сторон точками.
луч - это прямая линия, которая имеет начало, но не имеет конца.
угол - это геометрическая фигура, образованная 2-мя лучами
развернутый угол-это угол, стороны которого составляют прямую
2. если две стороны и угол между ними одного треугольника соответственно равны двум сторонам между ними другого треугольника, то такие треугольники равны
3. т.к. треугольник прямоугольный, а один из углов 30гр, то второй катет будет равен половине гипотенузы 12*2=24см
4.т.к треуг.АВС равноб. следовательно углы при основании равны, а т.к. угол 1 вертикальный углу ВАС, значит они равны
2 вертик угол ВС, а следовательно они равны
угол1 = углу ВАС, угол 2 - углу ВСА
следовательно углы =
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство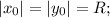
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)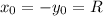 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и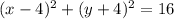
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили