15 ! определите центр и радиус окружности , заданной уравнением 1)x²-6x+y²+2y-6=0

2)x²+y²+10y+24=0

Так как окружность является описанной около треугольника , то его гипотенуза  является диаметром . . Пусть одна часть равна х, тогда гипотенуза  равна 5х, катет 3х, получим уравнение  (5 х) в квадрате =  16 в квадрате + (  3х)в квадрате - по теореме Пифагора. 

 Получаем 25 х в квадрате = 256 + 9х в квадрате.

                      16 х в квадрате = 256

                         х в квадрате = 16

                           х= 4  ; х= -4

 -4 не удовлетворяет условию задачи.

Найдём гипотенузу 5х= 5*4 = 20, гипотенуза это диаметр, значит радиус 20:2 =10

ответ : 10 см

ответ:SABCD=81√3см²

Объяснение:

SABCD=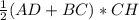

1.ΔADB(∠B=90°):

∠ADB=90-∠BAD=90-60=30°(Сумма острых углов прямоугольного треугольника равна 90)

AB=1/2AD=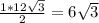см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)

2.Трапеция ABCD:

AB=CD=6√3см(В равнобокой трапеции боковые стороны равны)

∠A=∠D=60(В равнобокой трапеции  углы при основаниях равны)

3.ΔDCH(∠H=90°):

∠DCH=90-∠CDH=90-60=30°(Сумма острых углов прямоугольного треугольника равна 90)

HD=1/2CD=6√3/2=3√3см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)

sinCDH=CH/CD

CH=sinCDH*CD=sin60*6√3=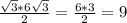см

4.Трапеция ABCD:

(Ссвойство равнобедренной трапеции)

AD-BC=2HD

-BC=-AD+2HD

BC=AD-2HD=12√3-2*3√3=12√3-6√3=6√3см

SABCD=см²