Гегель использует термин Mittelasien для обозначения области, населённой монголами. Термин «Средняя Азия» зафиксирован в трудах историка С. М. Соловьёва, под которым понимается степной географический регион к юго-востоку от Русской равнины и востоку от Каспийского моря.
В древности в Средней Азии существовали довольно крупные государства. В VII—V вв. до н. э. в долине Зарафшана существовало государство Согдиана, в среднем течении Амударьи — Бактрия, в нижнем её течении — Хорезм, в долине Мургаба — Маргиана. Северная часть Средней Азии входила в состав Скифии, а южная часть находилась в сфере влияния Ирана.
Первые сведения о Средней Азии встречаются в трудах Геродота, Страбона, Арриана, Птолемея и других.
Гегель использует термин Mittelasien для обозначения области, населённой монголами. Термин «Средняя Азия» зафиксирован в трудах историка С. М. Соловьёва, под которым понимается степной географический регион к юго-востоку от Русской равнины и востоку от Каспийского моря.
В древности в Средней Азии существовали довольно крупные государства. В VII—V вв. до н. э. в долине Зарафшана существовало государство Согдиана, в среднем течении Амударьи — Бактрия, в нижнем её течении — Хорезм, в долине Мургаба — Маргиана. Северная часть Средней Азии входила в состав Скифии, а южная часть находилась в сфере влияния Ирана.
Первые сведения о Средней Азии встречаются в трудах Геродота, Страбона, Арриана, Птолемея и других.
45°
Объяснение:
АВСД-ромб. АС⊥ВД. АС=40см. ВД=30см.
Из вершины В ромба АВСД проведём высоту ВК⊥ДС.
МК - наклонная, ВК - её проекция на плоскость АВСД.
По теореме о трёх перпендикулярах: МК⊥ДС.
∠МКБ - угол между плоскостью ромба и плоскостью CMD - искомый угол.
(Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.)
1) ΔОВС (∠О=90° - как угол между диагоналями ромба).
По т.Пифагора найдём сторону ромба:
ВС² = ВО²+ОС² = 15²+20²=625, ВС= 25 см
Т.е. АВ=ВС=СД=АД=25 см - как диагонали ромба
2) ΔВСД .
СО⊥ВД т.к. диагонали ромба пересекаются под прямым углом.
ВК⊥ДС по построению.
Площадь ΔВСД:
S =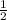
*ВД*ОС
S =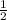
*ДС*ВК
⇒ВД*ОС=ДС*ВК; 30*20=25*ВК; ВК=30*20/25=24 см
3) Рассмотрим ΔМВК. МВ⊥ВК, МВ=ВК=24 см.
⇒ΔМВК - равносторонний прямоугольный треугольник.
∠КМВ =∠МКВ = 90°/2 = 45°