2. Сумма углов восьмиугольника вычисляется по формуле:
. Разделив это число на 8, найдем чему равен один угол. . По определению, внешний угол это угол, смежный с любым внутренним. А так как сумма смежных углов равна 180 градусам, получаем: , что и сходится с утверждением.
3. Разобьем параллелограмм на четыре треугольника путем проведения в нем диагоналей. Для произвольного треугольника на плоскости всегда выполняется неравенство треугольника: сумма длин двух сторон больше или равна длине третьей. Дальше все понятно, во вложении.
5. У правильного многоугольника с нечентым числом сторон осями симметрии являются прямые, выходящие из вершин углов, которые перпендикулярны противолежащей углам сторонам. Для правильного многоугольника точка пересечения этих прямых будет являться центром описанной окружности. А по свойству тех же правильных многоугольников, это точка будет еще и центром вписанной окружности. Следовательно, центр вписанной окружности является центром симметрии пятиугольника.
1. Дано: а⊥n, n - ось симметрии. Доказать: а→а Доказательство: Пусть О = а∩n. Отметим на прямой а произвольные точки А и В. Построим точки A', B', симметричные точкам А и В относительно оси n. Для этого проведем лучи с началом в точках А и В перпендикулярно n. Эти лучи будут лежать на прямой а, так как через точку можно провести единственный перпендикуляр к прямой. A' и B' будут лежат на этих лучах, а значит, на прямой а. Значит, прямая а отображается на себя.
2. Дано: прямая а, О - центр симметрии, О∈а. Доказать: а→а Доказательство: Отметим на прямой а точку А. Для построения А' проведем луч АО. Луч будет лежать на прямой а, следовательно, и A' будет лежать на прямой а. АО→OA' ⇒ прямая а отобразиться на себя.
2. Сумма углов восьмиугольника вычисляется по формуле: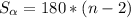
3. Разобьем параллелограмм на четыре треугольника путем проведения в нем диагоналей. Для произвольного треугольника на плоскости всегда выполняется неравенство треугольника: сумма длин двух сторон больше или равна длине третьей. Дальше все понятно, во вложении.
5. У правильного многоугольника с нечентым числом сторон осями симметрии являются прямые, выходящие из вершин углов, которые перпендикулярны противолежащей углам сторонам. Для правильного многоугольника точка пересечения этих прямых будет являться центром описанной окружности. А по свойству тех же правильных многоугольников, это точка будет еще и центром вписанной окружности. Следовательно, центр вписанной окружности является центром симметрии пятиугольника.
Дано: а⊥n, n - ось симметрии.
Доказать: а→а
Доказательство:
Пусть О = а∩n.
Отметим на прямой а произвольные точки А и В.
Построим точки A', B', симметричные точкам А и В относительно оси n. Для этого проведем лучи с началом в точках А и В перпендикулярно n.
Эти лучи будут лежать на прямой а, так как через точку можно провести единственный перпендикуляр к прямой. A' и B' будут лежат на этих лучах, а значит, на прямой а. Значит, прямая а отображается на себя.
2.
Дано: прямая а, О - центр симметрии, О∈а.
Доказать: а→а
Доказательство:
Отметим на прямой а точку А. Для построения А' проведем луч АО. Луч будет лежать на прямой а, следовательно, и A' будет лежать на прямой а.
АО→OA' ⇒ прямая а отобразиться на себя.