2 вариант 1. В треугольнике ABC угол С-90°. АС-4 см, АВ=5 см. Найдите
sin A, cos A, tgA, sin B, cos B, tgB..
2. В треугольнике ABC, ZC = 90°, проведена высота Сн из
вершины прямого угла, которая делит гипотенузу на отрезки
AH=18 см и HD= 2 см. Найти катеты треугольника и высоту,
проведенную из вершины прямого угла.
3. Найти площадь равнобедренного треугольника с углом 45
при основании, если боковая сторона равна 8 см.
4. В равнобедренной трапеции ABCD основания равны 5 см и
см. Диагональ BD перпендикулярна к боковой стороне AB.​

В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.

4√37 см

Объяснение:

∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит

ΔDSQ ~ ΔDFR по двум углам.

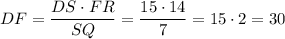см

 см²

Площадь треугольника DFR можно вычислить так же по формуле:

Из треугольника DFR по теореме косинусов:

DR² = 30² + 14² - 2 · 30 · 14 · 0,6

DR² = 900 + 196 - 504 = 592

DR = √592 = 4√37 см

W, V - центры

Проведем WK⊥AE, VL⊥AE

BK=1, DL=1 (перпендикуляр из центра к хорде делит ее пополам)

AK=3, AL=6

Проведем WN⊥VL

Понятно, что W - середина AV, N - середина VL

WK=VN=NL=x

Rw =WB =√(WK^2+BK^2) =√(x^2+1)

Rv =VD =√(VL^2+DL^2) =√(4x^2+1)

WV =Rw+Rv (точка касания лежит на линии центров)

WV =√(VN^2+WN^2) => Rw+Rv =√(x^2+9)

√(x^2+1) + √(4x^2+1) = √(x^2+9)

x^2 +1 +4x^2 +1 +2√(x^2+1)√(4x^2+1) = x^2 +9

4(x^2+1)(4x^2+1) = (7-4x^2)^2    // при 7-4x^2 >=0 => x<=√7/2

16x^4 +16x^2 +4x^2 +4 = 49 -56x^2 +16x^4

76x^2 = 45 => x=√(45/76)

Rw =√(45/76 +1) =√(121/76) =11/2√19

Rv =√(4*45/76 +1) =√(256/76) =8/√19