2. Знайти кути, що утворилися при перетині двох прямих, якщо:
а) один із них на 30° більший за інший;
б) сума трьох із цих кутів дорівнює 300°;
в) сума трьох із цих кутів більша за суму
двох із цих кутів на 60°.​

У колі з радіусами АО і ОВ пряма а проходить через середини радіусів так, що ОЕ = ОА/4. Оскільки відстань - це перпендикуляр, маємо прямокутний трикутник КОЕ та РОЕ. З прямокутного трикутника КОЕ: ОК = ОА/2, ОЕ = ОА/4. Тобто, катет ОЕ у два рази менший за гіпотенузу ОК. Катет, що дорівнює половині гіпотенузи, лежить проти кута 30 градусів. Тобто, кут ОКЕ = 30 градусів. Кут КОЕ = 90 - 30 = 60 градусів. Трикутники КОЕ та РОЕ рівні за прямим кутом та гіпотенузою, тобто кути КОЕ та РОЕ рівні і дорівнюють по 60 градусів. Кут АОВ = <KOE + <POE = 60 + 60 = 120 градусів.

ед²

Объяснение:

Дано: ABCD - параллелограмм.

AE = ED; DF = FC.

BE ∩ AC = G; BF ∩ AC = H;

S  (ABCD) = 12.

Найти:  S (GHFE)

1. Рассмотрим ΔABD и ΔDBC.

Любая диагональ параллелограмма делит его на два равных треугольника.

⇒ S (ΔABD) = S (ΔDBC) = 12:2 = 6

Аналогично:

S (ΔABC) = S (ΔACD) = 12:2 = 6

2. Рассмотрим ΔABD.

AE = ED (условие) ⇒ВЕ - медиана.

Медиана делит треугольник на два равновеликих треугольника.

⇒ S (ΔABE) = S (ΔEBD) = 6:2 = 3

3. Рассмотрим ΔDBC.

DF = FC ⇒ BF - медиана.

S (ΔDBF) = S(ΔFBC) = 6:2 = 3

4. Рассмотрим ΔACD.

AE = ED; DF = FC (условие)

⇒ EF - средняя линия.

Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвертой площади исходного треугольника.

⇒

5. Найдем площадь ΔEBF.

S (ΔEBF) = S (ABCD) - S(ΔABE) - S(ΔFBC) - S(ΔEFD) =

6. Рассмотрим ΔABD.

BF - медиана (п.3)

Диагонали параллелограмма точкой пересечения делятся пополам.

⇒ BO = OD ⇒ СО - медиана.

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

⇒ BH : HF = 2:1

или ВН : BF = 2:3

7. Рассмотрим ΔABD.

Аналогично п.6: BE и AO - медианы.

⇒BG : GE = 2 :1

или BG :BE = 2:3

8. Рассмотрим ΔGBH и ΔEBF.

∠B - общий. ВН : BF = 2:3 (п.6); BG :BE = 2:3 (п.7)

⇒ ΔGBH ~ ΔEBF, k =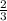

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Найдем площадь GHFE: