215. З точки D до площини ABC проведено пер- пендикуляр DA, DA = d (рис. 122). Похилі DB і DC утворюють зі своїми проекціями кути, рівні 30°, а іх проекції утворюють кут 120° Знайдіть довжину відрізка BC. ВС.
Пусть AB = 17x, AC = 8x. Тогда периметр треугольника 40 = 10,2 + 4,8 + 17х + 8х = 15 + 25х ⇒ х = 1 ⇒ AB = 17, AC = 8; BC = 10,2 + 4,8 = 15.
Заметим, что AC² + BC² = 8² + 15² = 289 = 17² = AB², то есть треугольник прямоугольный с прямым углом C по теореме, обратной теореме Пифагора. Его площадь .
∠AED = 180° - ∠CED = 180° - ∠A =
Треугольники ABC и EDC подобны по двум углам (∠C — общий, ∠A = ∠E по параллельности AB и DE).
1) AB = 17
2) S = 60
3) ∠AED =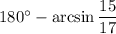
∠EDA =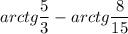
Объяснение:
По свойству биссектрисы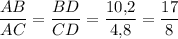
Пусть AB = 17x, AC = 8x. Тогда периметр треугольника 40 = 10,2 + 4,8 + 17х + 8х = 15 + 25х ⇒ х = 1 ⇒ AB = 17, AC = 8; BC = 10,2 + 4,8 = 15.
Заметим, что AC² + BC² = 8² + 15² = 289 = 17² = AB², то есть треугольник прямоугольный с прямым углом C по теореме, обратной теореме Пифагора. Его площадь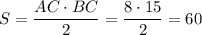 .
.
∠AED = 180° - ∠CED = 180° - ∠A =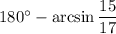
Треугольники ABC и EDC подобны по двум углам (∠C — общий, ∠A = ∠E по параллельности AB и DE).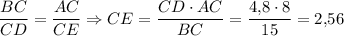
∠EDA = ∠CDA - ∠CDE =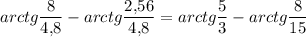
Дано: угол С равен 60°, AB=3, BC=8, CD=5.
Найти:
а) Длину BD. Находим по теореме косинусов.
BD = √(5² + 8² - 2*5*8*cos 60°) = √(25 + 64 - 2*5*8*(1/2) =
= √49 = 7.
б) Длину радиуса окружности.
R = (abc)/(4S). Площадь треугольника BCD определяем по Герону:
a = 5, b = 8, c = 7.
p = (5+8+7)/2 = 20/2 = 10.
S = √(10*5*2*3) = 10√3 ≈ 17, 320508.
R = (5*8*7)/(4*10√3) = 7/√3 = 7√3/3.
в) Площадь четырёхугольника ABCD.
Находим площадь треугольника ABD.
По теореме синусов находим AD = 5. p = (3 + 7 + 5)/2 = 7,5.
S(ABD) = √(7.5*4.5*0.5*2.5) = √42,1875 ≈ 6,495191.
S(ABCD) = 10√3 + √42,1875 ≈ 23,8157 кв.ед.