253. Скільки діагоналей можна провести з однієї вершини опуклого семикутника? Знайдіть загальну кількість діагоналей опуклого семикутника. и еще на фото №253,257,258,260,261 и все
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
Если в прямоугольном треугольнике известен катет и биссектриса, проведенная к гипотенузе, то в одном из двух получившихся треугольников будут известны две стороны и угол между ними (90/2=45). Этого достаточно, чтобы однозначно найти все оставшиеся стороны и углы (используя теоремы синусов и косинусов). Зная свойство биссектрисы: "биссектриса делит третью сторону треугольника пропорциональные двум другим сторонам", можно используя его совместно с теоремой Пифагора однозначно определить все стороны и углы этого прямоугольного треугольника. А это означает, что все прямоугольные треугольники с одинаковым катетом и биссектрисой, проведенной к гипотенузе равны. Надеюсь несмотря на большое количество текста, объяснил понятно :)
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство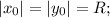 учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 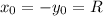
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и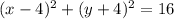
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
Надеюсь несмотря на большое количество текста, объяснил понятно :)