26. apoc – квадрат. внутри него построен равносторонний треугольник abc. на стороне
вс вне треугольника построен квадрат bcrt. лежат ли точки a, о и т на одной прямой?

решите

Показать ответ

Ответ:

эля792

18.03.2020 06:08

$3\sqrt{89}$

Объяснение:

Объём пирамиды:

$V=\frac{1}{3} S*h$ , где S - площадь основания, h - высота пирамиды.

Значит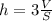 $h=3\frac{V}{S}$

У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.

Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.

Диагональ квадрата равна √(2а²)=а*√2,

тогда половина диагонали равна а/√2, а так как а=√S,

то половина диагонали равна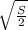 $\sqrt{\frac{S}{2} }$

Тогда, по теореме Пифагора:

$l=\sqrt{\frac{S}{2}+(3\frac{V }{S})^{2} }\\l=\sqrt{72+27^{2} } =\sqrt{72+729} =\sqrt{801} =3\sqrt{89}$

0,0(0 оценок)

Ответ:

MarinaSc1

04.07.2022 19:14

1)ответ:

V = 5√3/6 ед³.

Sбок = 144 ед².

Объяснение:

Судя по тому, что ∠АВС= 120°, параллелепипед не прямоугольный, а прямой. Это "две большие разницы".

Итак, высота параллелепипеда равна 9см, а в основании прямого параллелепипеда лежит параллелограмм со стороной ВС = 5 см, диагональю АС=7см и углом АВС = 120°. По теореме косинусов попробуем найти сторону АВ.

АС² =АВ²+ВС² - 2·АВ·ВС·Cos120. Cos120 = -Cos60 = - 1/2.

49 = AB²+25 - 2·AB·5·(-1/2) =>

АВ²+5·АВ -24 =0 => AB = 3cм

So = AB·BC·Sin120 = 3·5·√3/2.

V = So·h = (3·5·√3/2)·9 = 5√3/6 ед³. (площадь основания, умноженная на высоту).

Sбок = Р·h = 2(3+5)·9 = 144 ед² ( периметр, умноженный на высоту)

2)Обозначим радиус основания конуса R, высоту Н.

По заданию угол, тангенс которого равен Н/R, равен 30 градусов.

Н/R = tg30° = √3/3.

Отсюда Н = R√3/3 см.

Площадь сечения S = (1/2)*2R*H =RH = R*(R√3/3) = R²√3/3 см².

Приравняем по заданию: R²√3/3 = 9√3 см².