275. Шеңберден тыс жаткан В нүктесі арқылы шеңберге BM
(М-жанасу нүктесі) мен шенбердi C және D нүктелерінде (С нүктесі В мен D-ның арасында жатыр) қиятын киюшы жүргізілген.
BD= 12 см, ВМ=2 бөлінген 3 × CD екені белгілі болса, ВМ кесіндісінің,
ұзындығын табыңдар.​

Вариант 1.

Так как <ABC = 45°, то: <A = 90-45 = 45°.

И так как острые углы друг другу равны, то прямоугольный треугольник — равнобёдренный, тоесть: BC = AC.

//Росстояние от точки A  — до плоскости "α" — это и есть катет AC.//

У нас есть 2 условия: AB+BC = 17; AC-BC = 7.

И так как эти 2 катета равны — то составим систему только с одной переменной "x":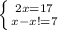

Э-э, стоп, что? Разность двух равных чисел не равна 7-и? Недопустимо!

Задача с ошибкой, если один и острых углов равен 45°, то второй тоже.  Катеты равны, тоесть их разность не может быть равной 7-и.

Вариант 2.

Проигнорируем определение острого угла 45-градусов, представим, что нам известно только это: AC+BC = 17; AC-BC = 7.

Этой информации нам достаточно, чтобы найти катеты.

Но только на этот раз — переменных будет 2: AC = "x"; BC = "y".

Вывод: AC = 12.

Даны координаты вершин трапеции ABCD: . Напишите уравнения прямых, содержащих

а) диагонали AC и BD;

б) среднюю линию трапеции.

Решение (рис. 1):

Рис. 1. Иллюстрация к задаче

общее уравнение прямой, оно задается конкретной тройкой чисел a, b и c.

а) Найдем уравнение прямой АС, для этого в уравнение прямой подставляем координаты точек А и С:

Как и раньше, получили два уравнения с тремя неизвестными, будем решать ее методом алгебраического сложения.

Если с=0, то прямая проходит через начало координат. Подставим с в любое уравнение:

б) Найдем уравнение прямой BD: точки B и D имеют одну и ту же ординату, равную 1, поэтому уравнение прямой BD.

в) Найдем координаты точки M – середины CD и точки N – середины AB:

Рис. 2. Иллюстрация к задаче

Подставляем координаты точек M и N в уравнение

Подставляем в первое уравнение: