Отношение катета МЕ и гипотенузы ВЕ=3:5, значит, второй катет⊿ МВЕ (египетского) равен 8 см (и по т.Пифагора ВМ=8 см). По условию ВС - перпендикуляр к плоскости треугольника, следовательно, перпендикулярен ВЕ и ВМ. Расстояние от точки до прямой равно длине отрезка, проведенного перпендикулярно из точки к этой прямой. ВМ⊥МЕ и является проекцией наклонной СМ. По т. о 3-х перпендикулярах СМ⊥МЕ и является искомым расстоянием. ВМ=8 см, СВ=6 см ⇒ ∆ ВСМ - египетский. СМ=10 см ( можно проверить по т.Пифагора).
Осьовим перерізом циліндра є прямокутник АВСD, сторони AВ=СD якого є твірними циліндра (їх довжина дорівнює висоті h циліндра), а інші дві сторони AD=BC – діаметри основ циліндра.
Отже, AВ=СD=h і AD=BC=d=2*r. r - радіус основи циліндра.
Площа прямокутника АВСD (осьового перерізу):
Sпер=АВ•ВС=h•d
Згідно умови r = h+1 ⇒ d = 2*r = 2h+2
ΔАВС - прямокутний (∠В=90°). За теоремою Піфагора маємо:
Отношение катета МЕ и гипотенузы ВЕ=3:5, значит, второй катет⊿ МВЕ (египетского) равен 8 см (и по т.Пифагора ВМ=8 см). По условию ВС - перпендикуляр к плоскости треугольника, следовательно, перпендикулярен ВЕ и ВМ. Расстояние от точки до прямой равно длине отрезка, проведенного перпендикулярно из точки к этой прямой. ВМ⊥МЕ и является проекцией наклонной СМ. По т. о 3-х перпендикулярах СМ⊥МЕ и является искомым расстоянием. ВМ=8 см, СВ=6 см ⇒ ∆ ВСМ - египетский. СМ=10 см ( можно проверить по т.Пифагора).
60 см²
Объяснение:
Осьовим перерізом циліндра є прямокутник АВСD, сторони AВ=СD якого є твірними циліндра (їх довжина дорівнює висоті h циліндра), а інші дві сторони AD=BC – діаметри основ циліндра.
Отже, AВ=СD=h і AD=BC=d=2*r. r - радіус основи циліндра.
Площа прямокутника АВСD (осьового перерізу):
Sпер=АВ•ВС=h•d
Згідно умови r = h+1 ⇒ d = 2*r = 2h+2
ΔАВС - прямокутний (∠В=90°). За теоремою Піфагора маємо:
АВ²+ВС²=АС²
h²+(2h+2)²=13²
5h²+8h-165=0
D=b²-4ac=64-4*5*(-165)=3364=58²
h₁ ₂ =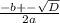 =
= 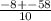
h₁ = 5
h₂ = -6.6 - ∅
h = 5 см,
d = 2h+2 = 2*5+2 = 12 см
Sпер=h•d = 5*12=60 см²