3. В окружности с центром О проведен диаметр KC = 10, 4cm , пересекающий хорду АВ в точке Р, причем Р середина хорды. Угол между диаметром и радиусом равен 30° Найдите длину хорды AB и Периметр /_\АОВ
ответ: доказать это невозможно. Объясняю: рисуем угол, проводим его биссектрису, берем на ней точку P. Проводим окружность с центром в точке P так, чтобы она каждую сторону угла пересекала в двух точках. Пусть на одной стороне это точки M_1 и M_2 (M_1 ближе к вершине угла, M_2 дальше), на второй -K_1 и K_2 (K_1 ближе к вершине угла, K_2 дальше). Если из точек M_1, M_2 выбрать, скажем M_1, а из точек K_1, K_2 выбрать K_2, то DM_1≠DK_2, хотя все условия задачи выполнены.
Эта ситуация является хорошей иллюстрацией, почему есть признак равенства треугольников по двум сторонам и углу между ними, но нет признака по двум сторонам и углу не между ними (то есть такой признак можно было бы придумать, но пришлось бы давать дополнительную информацию, скажем по поводу того, являются ли наши треугольники остроугольными или тупоугольными)
Рассмотрим ромб. (лучше нарисовать для наглядности)
Начертим диагонали. Так как все стороны равны у нас получаются равнобедренные треугольники.
Так как треугольники равнобедренные, тогда так как диагонали пересекаются под прямым углом, получается, что она является так же биссектрисой, следовательно, если рассмотреть прямоугольный треугольник, у нас получатся углы 30, 90 градусов. Свойство прямоугольного треугольника - против стороны в 30 градусов, лежит катет равный половине гипотенузы, следовательно сторона будет равна 10.
Получается, что диагональ, которая является меньше = 10 * 2 = 20 см.
№2
Рассмотрим треугольник, который образуется при проведении высоты из точки B. У нас образуется треугольник с углами 90 и 45. Вычислим оставшийся угол. 180 - 90 - 45 = 45 градусов.
У нас получается равнобедренный прямоугольный треугольник.
Чтобы узнать катеты треугольника надо вспомнить теорему Пифагора
с^2 = K1^2+K2^2
получается 49 = 2*K^2
K^2 = 49:2 = 24,5
Катет будет равен
№3
Рассмотрим трапецию. Угол ACB = углу CAD = 37, так как как крест лежащий угол при параллельных прямых BC и AD.
Объясняю: рисуем угол, проводим его биссектрису, берем на ней точку P. Проводим окружность с центром в точке P так, чтобы она каждую сторону угла пересекала в двух точках. Пусть на одной стороне это точки M_1 и M_2 (M_1 ближе к вершине угла, M_2 дальше), на второй -K_1 и K_2 (K_1 ближе к вершине угла, K_2 дальше).
Если из точек M_1, M_2 выбрать, скажем M_1, а из точек K_1, K_2 выбрать K_2, то DM_1≠DK_2, хотя все условия задачи выполнены.
Эта ситуация является хорошей иллюстрацией, почему есть признак равенства треугольников по двум сторонам и углу между ними, но нет признака по двум сторонам и углу не между ними (то есть такой признак можно было бы придумать, но пришлось бы давать дополнительную информацию, скажем по поводу того, являются ли наши треугольники остроугольными или тупоугольными)
1) ответ 20 см.
2) ответ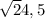
3) ответ 128 градусов
Объяснение:
№1
Рассмотрим ромб. (лучше нарисовать для наглядности)
Начертим диагонали. Так как все стороны равны у нас получаются равнобедренные треугольники.
Так как треугольники равнобедренные, тогда так как диагонали пересекаются под прямым углом, получается, что она является так же биссектрисой, следовательно, если рассмотреть прямоугольный треугольник, у нас получатся углы 30, 90 градусов. Свойство прямоугольного треугольника - против стороны в 30 градусов, лежит катет равный половине гипотенузы, следовательно сторона будет равна 10.
Получается, что диагональ, которая является меньше = 10 * 2 = 20 см.
№2
Рассмотрим треугольник, который образуется при проведении высоты из точки B. У нас образуется треугольник с углами 90 и 45. Вычислим оставшийся угол. 180 - 90 - 45 = 45 градусов.
У нас получается равнобедренный прямоугольный треугольник.
Чтобы узнать катеты треугольника надо вспомнить теорему Пифагора
с^2 = K1^2+K2^2
получается 49 = 2*K^2
K^2 = 49:2 = 24,5
Катет будет равен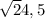
№3
Рассмотрим трапецию. Угол ACB = углу CAD = 37, так как как крест лежащий угол при параллельных прямых BC и AD.
Угол B = 180 - 15 - 37 = 128 градусов