AM - медиана треугольника ABC, то BE = EC = BC/2 = AE/2.
Сделаем дополнительное построение, т.е. построим до параллелограмма ABDC, в нём AD = 2AE = 2BC, тогда сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
Не трудно заметить, что треугольник ABC - прямоугольный с гипотенузой AB = √7 и катетами AC = √3; BC = 2.
2) Площадь треугольника: кв. ед.
3) Центр описанной окружности лежит на середине гипотенузы, значит радиус описанной окружности равен половине гипотенузы.
Теорема синусов: в треугольнике отношение стороны к синусу противолежащего угла - величина постоянная. a : sin α = b : sin β sinβ = b · sin α / a По найденному синусу угла по таблице находим угол.
1) a = 3 м , b = 5 м , α = 30 ° sin β = 5 · sin 30° / 3 = 5 · 1/2 / 3 = 5/6 ≈ 0,8333 β ≈ 56°
2) a = 8 м , b = 7 м , α = 60° sin β = 7 · sin 60° / 8 = 7 · √3/2 /8 = 7√3/16 ≈ 0,7578 β ≈ 49°
3) a = 2√2 см , b = 3 см , α = 45° sin β = 3 · sin 45° / (2√2) = 3 · √2/2 / (2√2) = 3/4 = 0,75 β ≈ 49°
4) a = 6 см , b = 2√3 см , α = 120° sin β = 2√3 · sin 120° / 6 = √3 · (√3/2) / 3 = 3 / 6 = 1/2 = 0,5 β = 30°
Пусть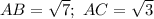 . Из условия AE = BC, а так как
. Из условия AE = BC, а так как
AM - медиана треугольника ABC, то BE = EC = BC/2 = AE/2.
Сделаем дополнительное построение, т.е. построим до параллелограмма ABDC, в нём AD = 2AE = 2BC, тогда сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
Не трудно заметить, что треугольник ABC - прямоугольный с гипотенузой AB = √7 и катетами AC = √3; BC = 2.
2) Площадь треугольника: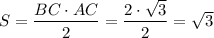 кв. ед.
кв. ед.
3) Центр описанной окружности лежит на середине гипотенузы, значит радиус описанной окружности равен половине гипотенузы.
a : sin α = b : sin β
sinβ = b · sin α / a
По найденному синусу угла по таблице находим угол.
1) a = 3 м , b = 5 м , α = 30 °
sin β = 5 · sin 30° / 3 = 5 · 1/2 / 3 = 5/6 ≈ 0,8333
β ≈ 56°
2) a = 8 м , b = 7 м , α = 60°
sin β = 7 · sin 60° / 8 = 7 · √3/2 /8 = 7√3/16 ≈ 0,7578
β ≈ 49°
3) a = 2√2 см , b = 3 см , α = 45°
sin β = 3 · sin 45° / (2√2) = 3 · √2/2 / (2√2) = 3/4 = 0,75
β ≈ 49°
4) a = 6 см , b = 2√3 см , α = 120°
sin β = 2√3 · sin 120° / 6 = √3 · (√3/2) / 3 = 3 / 6 = 1/2 = 0,5
β = 30°