2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC. . AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
S=132 cм2.
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы , где - угол между сторонами a и b. Значит . . Теперь умножим эту площадь на 8. Получим .
2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC.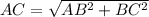
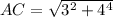. AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы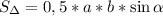
, где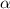 
- угол между сторонами a и b. Значит 
. 
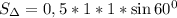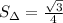
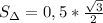. Теперь умножим эту площадь на 8. Получим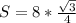 
.
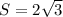Формула объёма шара V=4πR³:3
Формула объёма конуса V=S•H:3=πr²H:3а
Осевое сечение данного конуса - равносторонний треугольник, т.к. его образующая составляет с плоскостью основания угол 60°.
Выразим радиус r конуса через радиус R шара.
r=2R:tg60°=2R/√3
V(кон)=π(2R/√3)²•2R²3=π8R³/9
V(шара)=4πR³/3
V(кон):V(шар)=[π8R³/9]:[4πR³/3]=(π•8R³•3/9)•4πR³=2/3
———————
2) Формула объёма цилиндра
V=πr²•H
Формула площади осевого сечения цилиндра
S=2r•H
Разделим одну формулу на другую:
(πr²•H):(2r•H)=πr/2⇒
96π:48=πr/2⇒
4π=πr
r=4
Из площади осевого сечения цилиндра:
Н=S:2r=48:8=6
На схематическом рисунке сферы с вписанным цилиндром
АВ- высота цилиндра, ВС - его диаметр,
АС - диаметр сферы.
АС=√(6²+8²)=√100=10
R=10:2=5
S(сф)=4πR8=4π•25=100π см²
Объяснение: