4.9. Как расположены две окружности (0,; r ) и 0 (0,;
r,), у которых: 1) r = 6 см, r, = 15 см, 0,0, = 21 см; 2) r, = 12 см,
r, = 14 см, 0,0, = 8 см; 3) r = 6 см, r, = 5 см, 0,0, = 18 см?
2​

А) могут. например прямая а лежит в плоскости а, но не параллельна l, а прямая b лежит в плоскости а параллельно l; в этом случае прямые а и b пересекаются в пределах плоскости а
б) могут, например прямая а лежит в плоскости а не параллельно l, а прямая b лежит в плоскости b параллельно пересечению плоскостей; в этом случае прямые а и b скрещивающиеся
в) и та, и ругая - не могут; прямая а в любом случае пересекает обе плоскости одновременно, так как является пересекающейся с пересечением двух плоскостей; прямая b, будучи параллельна пересечению плоскостей l , может только лежать в одной из этих плоскостей полностью, либо лежать вне обеих плоскостей в целом, а в точке она пересекать ни одну из плоскостей не может.

Объяснение:

По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые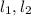 параллельные AB. Пусть 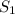-- плоскость, содержащая одновременно 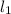и AB (эта плоскость существует из определения). Аналогично определяем плоскость 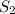. Заметим, что 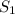и 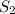проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости 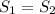= S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые 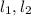. Причем, 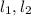проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит 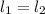, ч.т.д.