4. Каково наибольшее число отрезков, на которые делится отрезок АВ двумя пересекающими его прямыми?
А) 3;
Б) 4;
В) 5;
г) 6.
5. Каково наибольшее число частей, на которые три прямые разбивают
плоскость?
А) 4;
Б) 5;
В) 6;
Г) 7.​

Эта задача на много проще, чем кажется.
Если из центра окружности (который лежит на гипотенузе) опустить перпендикуляры на катеты, то получится квадрат и два треугольника, подобных исходному. Если обозначить радиус окружности r, больший катет большего треугольника b, меньший катет меньшего треугольника a,
то стороны исходного треугольника будут такие
(a + r, b + r, 35)
стороны меньшего треугольника
(a, r, 15)
стороны большего
(r, b, 20)
и все эти три треугольника подобны между собой.
отсюда a/r = 15/20 = 3/4;
то есть все эти три треугольника - египетские (подобные треугольнику со сторонами 3, 4, 5)
То есть уже можно написать ответ :) вычислять уже ничего не надо, надо просто "подобрать" коэффициенты подобия, чтобы гипотенузы египетских треугольников были бы 15 и 20. Само собой, это 3 и 4.
То есть a = 9, r = 12, b = 16; (получились треугольники 9, 12, 15 и 12, 16, 20)
Исходный треугольник имеет стороны 21, 28, 35, его площадь 294;
длина полуокружности πr = 12π;

Весь "трюк" в том, что r - одновременно больший катет в одном из подобных треугольников и меньший - в другом.

Объяснение:

Найдем гипотенузу АВ по Пифагору:

AB^2 = AC^2+BC^2 = 27+9= 36, отсюда гипотенуза АВ = 6

У описанной окружности, диаметром будет гипотенуза. Значит

радиус описанной окружности R=3

Радиус вписанной окружности r = (a+b-c)/2 = 1,5(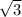+1)-3 (a  и b катеты, с - гипотенуза)

Против угла А лежит катет ВС, равный половине гипотенузы.

Значит <A = 30°  а <B = 90°-30° = 60°

Сектор, содержащий хорду АС имеет угловую величину центрального угла АОС = 2-<B = 2*60 = 120°, значит площадь сектора в 3 раза меньше площади круга

S=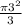 = 3π Отнимем отсюда площадь треугольника АОС и получим площадь сегмента

S(AOC) = 0,5S(ABC)=0,5*0,5*AC*BC = 0,25*3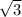*3 = 2,25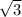

S(сег) = S - S(АОС) = 3π - 2,25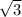 = 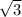(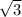π-2,25)