В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
=√147 см
Боковые грани правильной пирамиды это равные треугольники.
Угол GMB и угол GMN смежные, те их сумма равна 180гр, находим угол GMN = 180-уголGMB = 180-84=96гр
Сумма углов треугольника равна 180гр. К тому же угол MGN равен 1/2 угла МNG, тк это равнобедренный треугольник, а GM является биссектрисой. Таким образом мы можем записать, что 180=уголGMN+уголMNG+1/2углаMNG
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=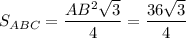 =9√3 см².
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=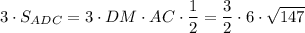 =9√147 см²
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
Сумма углов треугольника равна 180гр. К тому же угол MGN равен 1/2 угла МNG, тк это равнобедренный треугольник, а GM является биссектрисой. Таким образом мы можем записать, что 180=уголGMN+уголMNG+1/2углаMNG
То есть: 180=96+3/2углаMNG
3/2углаMNG=180-96
3/2углаMNG=84
Угол MNG = 56
Угол MNG = Угол BGN =56гр
Находим угол NBG:
180-уголMNG-уголBGN
180-56-56=68гр
ответ: угол N и угол G равны 56гр, угол B равен 68гр