Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 = (кв.ед.)
Из формулы площади шестиугольника S= выражаем сторону а:
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
Проведем МА⊥α и МВ⊥β. МА = 12 - расстояние от М до α, МВ = 16 - расстояние от М до β.
Пусть плоскость АМВ пересекает ребро двугранного угла - прямую а - в точке С. МА⊥α, а⊂α, значит МА⊥а. МВ⊥β, а⊂β, значит МВ⊥а. Так как прямая а перпендикулярна двум пересекающимся прямым плоскости АМВ, то она перпендикулярна этой плоскости, следовательно она перпендикулярна каждой прямой, лежащей в этой плоскости, ⇒ а⊥АС, а⊥ВС, ⇒∠АСВ = 90° - линейный угол двугранного угла; а⊥МС, ⇒ МС - искомое расстояние.
Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =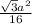
(кв.ед.)
Из формулы площади шестиугольника S=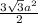
выражаем сторону а:
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
МА = 12 - расстояние от М до α,
МВ = 16 - расстояние от М до β.
Пусть плоскость АМВ пересекает ребро двугранного угла - прямую а - в точке С.
МА⊥α, а⊂α, значит МА⊥а.
МВ⊥β, а⊂β, значит МВ⊥а.
Так как прямая а перпендикулярна двум пересекающимся прямым плоскости АМВ, то она перпендикулярна этой плоскости, следовательно она перпендикулярна каждой прямой, лежащей в этой плоскости, ⇒
а⊥АС, а⊥ВС, ⇒∠АСВ = 90° - линейный угол двугранного угла;
а⊥МС, ⇒ МС - искомое расстояние.
МАСВ - прямоугольник, АС = МВ = 16.
Из прямоугольного треугольника АМС по теореме Пифагора:
МС = √(МА² + АС²) = √(16² + 12²) = √(256 + 144) = √400 = 20