5. Суреттерге минералдык ресурстарды игерумен байланысты болатын табиғи кешеніндегі
егерістер бейнеленген. Осы реттердегі өнеріске бата берiн.
а Казакстаннын да алмагында кездесетінін аныктанып,
b. Қалыптасу себебін талданып
с. Бұл өзгеріс несимен каунт?
а Мелені шешудан бир аъолын ұсыныңыз.​

тетради под рукой нет, напишу так

Объяснение:

1. Углы АВО и ВАО равны между собой --> 40. Тогда угол О равен 180-40-40= 100.

Получается угол С равен 80.

2. Проведи две касательные, из центра опусти перпендикуляры на касательные, это точки касания .Пусть точки Р и К. Тогда Треуг. OPA прямоуг. и OP=4,5,OA=9, тогда угол PAO=30(PO<AO в два раза). Треуг. OAK=треуг. OAP

угол OAK=30, получаем угол PAK=60 гр.

3. т.к АВ касательная ,следовательно ОВ перпендекулярна АВ  

Рассмотрим треугольник АОВ,  зная что угол О=60 градусов ,найдем АВ через тангенс угла О . tg(тангенс)угла О=АВ/ОВ, отсюда выразим АВ.

АВ= ОВ*tg угла О=12*tg 60 градусов=12* корень из трех=12корень из трех.

(см. объяснение)

Объяснение:

Рассмотрим плоскость (AST). Заметим, что BC⊥(AST), так как BC⊥SO и BC⊥AT и SO∩AT=O. Тогда BC перпендикулярна любой прямой, лежащей в этой плоскости. Опустим теперь перпендикуляр AH из точки A на ST в плоскости (AST). Получим, что AH⊥ST и AH⊥BC и ST∩BC=T. Тогда AH⊥(BSC), т.е. является искомым расстоянием. Найдем теперь AH. Приравняв площади треугольника, получим, что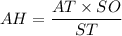 . Понятно, что AT ищем по теореме Пифагора для треугольника ATC: AT²=AC²-TC², => AT=4√3. ST ищем по той же теореме Пифагора, но для треугольника STC: ST²=SC²-TC² => ST=2√21. Перед тем, как искать SO, вспомним, что медианы точкой пересечения делятся 2:1, считая от вершины. Тогда OT=4/√3 => SO=2√177/3 (опять-таки по теореме Пифагора для треугольника OST). Значит 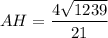. Приведем теперь ответ к требуемому виду: .

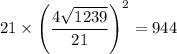Задание выполнено!