В прямоугольной системе координат даны векторы а {3; -2} и b{1; -2}. Найдите координаты вектора с=5а- 9b и его длину. Постройте вектор с , если его конец совпадает с точкой М(3;2). Решение. Умножение вектора на число: pa=(px1;py1), где p - любое число. Тогда Вектор 5a{15;-10} Вектор 9b{9;-18} Разность векторов : a-b=(x1-x2;y1-y2). Тогда Вектор c{6;8}. Длина вектора (его модуль) |c|=√(x²+y²). Тогда |c| = √(36+64) =10. Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат КОНЦА отнять соответствующие координаты НАЧАЛА. Зная координаты конца вектора, находим его начало: то есть 6=3-х, 8=2-y, откуда находим точку начала вектора с: Р(-3;-6). Зная координаты начала и конца вектора, легко построить его на координатной плоскости. (смотри рисунок).
Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол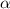
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.
Решение.
Умножение вектора на число: pa=(px1;py1), где p - любое число. Тогда
Вектор 5a{15;-10}
Вектор 9b{9;-18}
Разность векторов : a-b=(x1-x2;y1-y2). Тогда
Вектор c{6;8}.
Длина вектора (его модуль) |c|=√(x²+y²). Тогда
|c| = √(36+64) =10.
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат КОНЦА отнять соответствующие координаты НАЧАЛА.
Зная координаты конца вектора, находим его начало:
то есть 6=3-х, 8=2-y, откуда находим точку начала вектора с: Р(-3;-6).
Зная координаты начала и конца вектора, легко построить его на координатной плоскости. (смотри рисунок).