6. дано вектори а = (3; 5; 2), 5=(-1; -2: 1), 7 = (-2; 4; — 3). довести, що вони утворюють базис.знайти розклад вектора d = (1, 3, 14) за векторами а b c
Пусть x° равен смежный ∠ 2, тогда ∠ 1 равен (55+x)˚. Зная, что свойство смежных углов всегда содержит сумму 180°, составим уравнение с переменными и решим задачу алгебраическим
Составление математической модели:
Работа с математической моделью:
Поскольку уравнение имеет переменные, раскроем скобки и найдём значение переменных:
Теперь, зная что число с переменной и число без переменной в данном случае вычислить невозможно, перенесем число без переменной в правую часть уравнения (число становится отрицательным):
Затем вычислим полученный пример, находящийся в правой части уравнения:
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:
ответ математической модели:
Исходя из значения данного примера, получим корень уравнения:
Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров.
Для остроугольного треугольника этот центр будет в треугольнике.
Построение.
Построить нужный треугольник не составляет труда.
1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. .
Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности.
Расстояние от него до вершин треугольника равны радиусу описанной окружности.
2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника.
3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны.
∠ 1 = ?°, на 55° больше, чем ∠ 2.
∠ 2 = ?°
Оба угла являются смежными.
Решение:Пусть x° равен смежный ∠ 2, тогда ∠ 1 равен (55+x)˚. Зная, что свойство смежных углов всегда содержит сумму 180°, составим уравнение с переменными и решим задачу алгебраическим
Составление математической модели:
Работа с математической моделью:
Поскольку уравнение имеет переменные, раскроем скобки и найдём значение переменных:
Теперь, зная что число с переменной и число без переменной в данном случае вычислить невозможно, перенесем число без переменной в правую часть уравнения (число становится отрицательным):
Затем вычислим полученный пример, находящийся в правой части уравнения:
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:
ответ математической модели:
Исходя из значения данного примера, получим корень уравнения:
Теперь остаётся только узнать величину ∠ 1:
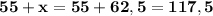˚ - ∠ 1.
Проверка: 117,5° + 62,5° = 180° - задача решена верно.ответ: ∠ 1 = 117,5°; ∠ 2 = 62,5°.Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров.
Для остроугольного треугольника этот центр будет в треугольнике.
Построение.
Построить нужный треугольник не составляет труда.
1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. .
Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности.
Расстояние от него до вершин треугольника равны радиусу описанной окружности.
2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника.
3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны.
Как это выглядит, дано в приложении.