Действительно, звезды не распределены по Вселенной равномерной «взвесью», они собираются в обширные группы — галактики. К примеру, наше Солнце находится в галактике Млечный Путь, а всего только в нем насчитывается около 100 млрд звезд. Но ведь одних только галактик в мироздании триллионы!Древний мудрец говорил, что пытаться сосчитать звезды равносильно тому, чтобы счесть все песчинки всех берегов на всей Земле. Но если нам не нужно точное число, а достаточно приблизительной оценки, то можно взять спутниковые снимки, установить примерно общую площадь подходящей береговой линии, узнать среднюю толщину песчаного слоя и, зная объем всего песка на Земле, разделить его на средний объем песчинки. Грубую цифру получить не но возможно.Если вернуться на небеса, то такими «пляжами» для нас могут выступать галактики: приблизительно установлено, что в нашей галактике 1011−1012звезд, а во Вселенной — 1011−1012 галактик подсчет показывает, что в мироздании должно быть 1022−1024 звезд.Это, конечно, грубая цифра, предполагающая, что наша галактика — весьма средняя, что отклонений от средней величины мало, и что мы верно оценили число галактик во Вселенной. А последнее может оказаться весьма обманчивой величиной, ведь долгое время считалось, что существует около 50 млрд галактик, и только работа орбитального телескопа Hubble увеличила эту цифру в 2,5 раза!И даже Hubble видит далеко не все. Не считая особенно удаленных или тусклых галактик, многие из них по невидимы для телескопа, работающего в оптическом диапазоне: они затемнены плотным газопылевым облаком, которое сопровождает процесс активного формирования звезд. Заглянуть в эти дали позволит уже инфракрасный зондHerschel, который готовится к запуску этой весной (о том, как он будет работать, мы рассказывали в заметке «Глазастый»).При этом стоит учесть, что никто и никогда в действительности не брался подсчитать число звезд в галактике: обычно замеряется какая-нибудь обобщающая характеристика, в частности, светимость галактики. Затем мы можем, грубо говоря, разделить светимость галактики на среднюю светимость звезды на таком же расстоянии — и оценить число звезд в ней. Примерно таким образом будет работать и Herschel, «подсчитывая» галактики и замеряя их светимость в ИК-диапазоне.Так что надо подождать — пока можно сказать, что звезд не меньше приведенной выше величины: 1 000 000 000 000 000 000 000 000, то есть триллион триллионов.
Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
Площадь одного треугольника будет равна:
Площадь шестиугольника:
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона = ; описанный - ΔA₁B₁C₁, сторона -
A1.
Sшестиугольника =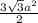
ответ: 4
A2.
Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
Площадь одного треугольника будет равна:
Площадь шестиугольника:
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона = ; описанный - ΔA₁B₁C₁, сторона -
; описанный - ΔA₁B₁C₁, сторона - 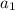
Для ΔA₁B₁C₁ радиус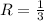 высоты
высоты 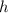
⇒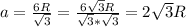
Для ΔABC радиус R =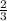 высоты
высоты 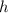 :
:
⇒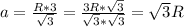
Найдем соотношение периметров и площадей: