7. Площина а паралельна стороні АВ трикутника AMB та перетинає сторони AM i BM у точ- ках А і В, відповідно. Знайдіть довжину сторони AM, якщо Ав1 = АА, = 2 см, AB = 6 см.
ДО ТЬ ДУЖЕ

1) CB = AB = 8, AC = 8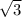, <A = <C = 30 <B = 120

2) 400 * sin113 * sin53 / sin14

3) AC =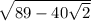

<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB  )

<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB  )

Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе

Объяснение:

1) <C = 180-120-30 = 30 значит треугольник ABC равнобедренный с основанием AC. CB = AB = 8. Пусть BD высота, она же медиана.

<DBA = 120 / 2 = 60. AD = AB * sin<DBA = 8*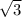 /2 = 4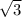

AC = 2AD = 8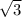

2) BC = AC * sinA / sinB

S = AC * BC * sinC / 2 = 20* 20 * sin113 * sin53 / sin14

3) AC =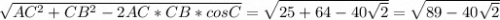

так как все стороный найдены можно подставить их значения в формулы:

<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB  )

<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB  )

Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе

Пирамида

Пирамидой называется многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников с общей вершиной, называемых боковыми гранями пирамиды. Пирамида называется n-угольной, если ее основанием является n-угольник.

Пирамида называется правильной, если её основание — правильный многоугольник и все боковые ребра равны.

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию. Усечённая пирамида называется правильной, если пирамида, из которой она была получена — правильная.

Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие в

Объяснение: