Проведем в треугольнике ABC высоту BH (она является еще и медианой, биссектрисой, т.к. треугольник равнобедренный).
Углы треугольника при основании (180/120)/2=30 гр.
Рассмотрим прямоугольный треугольник ABH. Катет BH лежит против угла в 30 гр. значит он равен 1/2*5=2,5. По теореме Пифагора найдем второй катет AH=√5^2-2,5^2=√25-6,25=√18,75=(5√3)/2
Диаметр описанной окружности равен 2S/p, где S-площадь, а p-полупериметр.
Объяснение:
Так как призма прямая, то длина ее высоты равна длине бокового ребра призмы.
Площадь боковой поверхности призмы равна:
S(бок) = S(AA₁C₁C) + S(BB₁C₁C) + S(AA₁B₁B)
Найдем боковую сторону равнобедренного треугольника в основании призмы:
Проведем высоту BH равнобедренного треугольника ABC с основанием AC.
По свойству высоты равнобедренного треугольника, проведенной к основанию, BH будет медианой, поэтому AH = CH = AC/2 = 4 см
По теореме Пифагора найдем AB:
AB =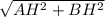 =
= 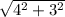 = 5
= 5
S(AA₁C₁C) = AA₁ * AC = 6 * 8 = 48 см²
S(BB₁C₁C) = BB₁ * BC = 6 * 5 = 30 см²
S(AA₁B₁B) = AB * AA₁ = 5 * 6 = 30 см²
S(бок) = 48 см² + 30 см² + 30 см² = 108 см²
Проведем в треугольнике ABC высоту BH (она является еще и медианой, биссектрисой, т.к. треугольник равнобедренный).
Углы треугольника при основании (180/120)/2=30 гр.
Рассмотрим прямоугольный треугольник ABH. Катет BH лежит против угла в 30 гр. значит он равен 1/2*5=2,5. По теореме Пифагора найдем второй катет AH=√5^2-2,5^2=√25-6,25=√18,75=(5√3)/2
Диаметр описанной окружности равен 2S/p, где S-площадь, а p-полупериметр.
Площадь треугольника равна 2,5*2*(5√3)/2/2=6,25√3
Полупериметр равен (5+5+5√3)/2=10+5√3/2
d=2*6,25√3/10+5√3/2=10√3-15