A(1; 2; 3), B(-1; 0; 1;), C(3; 3; 0) и D(3; -1; 2). Нарисуйте эти точки в прямоугольной системе координат. Определите точки, соответствующие осям и плоскостям.

Показать ответ

Ответ:

Dashatatur1

28.05.2021 07:19

Высота в равнобедренном треугольнике делит его на два равных прмоугольных треугольника. При этом, высота разбивает основание не две равные части, и они равны 18/2=9 см. В треугольнике ВДС по теореме Пифагора

$BC= \sqrt{BD^{2}+BC^{2}$

$BC= \sqrt{12^{2}+9^{2}\\$

$BC= \sqrt{225}\\$

ВС=15.

Так как треугольник равнобедренный, то АС=ВС=15.

Радиус вписанной окружности -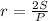 $r=\frac{2S}{P}$ , радиус описанной окружности - [tex 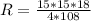$R=\frac{15*15*18}{4*108}$ ]R=\frac{abc}{4S}[/tex].

Периметр треугольника равен 15*2+18=48 см. Площадь треугольника по формуле Герона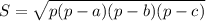 $S=\sqrt{p(p-a)(p-b)(p-c)$ , гдер - полупериметр, равный 48/2=24 см.

$S=\sqrt{(24*(24-15)^{2}(24-18)$

$S=\sqrt{(6*4*9^{2}*6$

S=6*2*9=108 см^2

Теперь мы можем найти радиусы:

$r=\frac{2*108}{48}$

r=4.5 cм

$R=\frac{15*15*18}{4*108}$

R=9.375 см.

ответ: радиус вписанной окружности - 4,5см, радиус оаписанной окружности 9,375 см. ;)

0,0(0 оценок)

Ответ:

iSia07

18.07.2022 08:21

1)При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.

АМ + МВ = 20²

АМ*МВ = 36 (так как 4*9 = 36) Тогда МВ² - 20МВ +36 =0 МВ = (20±16):2 = 18 или 2.

То есть точка М делит диаметр на отрезки 18 и 2 (18*2 =36 - проверка)

2) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

тогда имеем трапецию, образованную расстояниями от концов любого диаметра до этой косательной и среднюю линию этой трапеции в виде ее радиуса.

Но средняя линия параллельна основаниям и равна их полусумме, то есть полусумма расстояний до касательной это радиус, а сумма - диаметр этой окружности, что и требовалось доказать

0,0(0 оценок)

Популярные вопросы: Геометрия