Геометрия: A||b c-секущая угол 2 равно 78 градусов угол 1

A||b c-секущая угол 2 равно 78 градусов угол 1

Показать ответ

Ответ:

Latimel

17.06.2021 15:48

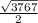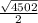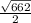а) 217/264, 287/324, -551/1188; б) $\frac{\sqrt{3767}}{2}$ , $\frac{\sqrt{4502} }{2}$ , $\frac{\sqrt{662} }{2}$ .

Объяснение:

Не выяснили, чем всё-таки являются числа в условии, так что я приму их за длины сторон треугольника АВС, где АВ=27, ВС=22, АС=42.

Здесь пригодится теорема косинусов: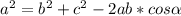 $a^{2} =b^{2} + c^{2} -2ab*cos\alpha$ , где угол альфа - угол напротив стороны а.

Применим теорему для стороны АВ: АВ²=ВС²+АС²-2ВС*АС*cosBCA

27²=22²+42²-2*22*42*cosBCA

729=484+1764-1848cosBCA

1848cosBCA=1519

cosBCA=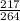 $\frac{217}{264}$

Аналогично применяем теорему для оставшихся углов и получаем:

cosСАВ=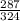 $\frac{287}{324}$

cosСВА= -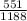 $\frac{551}{1188}$

Чтобы дальше решать было удобнее, обозначим точки пересечения медиан и сторон треугольника: медиана из угла А пересекает сторону СВ в точке К, медиана из угла В пересекает сторону АС в точке L, а медиана из угла С пересекает сторону АВ в точке М. Теперь вычислим длины медиан. Как известно, медианы делят стороны, к которым проведены, пополам. Таким образом получаем: AL=LC=42/2=21, CK=KB=22/2=11, BM=MA=27/2=13,5.

Здесь опять нужна теорема косинусов, только теперь необходимо найти одну из сторон при известном косинусе и двух других сторонах.

СМ²=АС²+АМ²-2АМ*АС*cosСАВ

СМ²=42²+13,5²-2*13,5*42*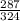 $\frac{287}{324}$

СМ=√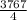 $\frac{3767}{4}$

СМ=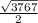 $\frac{\sqrt{3767}}{2}$

Аналогично поступаем и с другими медианами:

АК=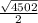 $\frac{\sqrt{4502} }{2}$

BL=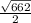 $\frac{\sqrt{662} }{2}$

Дано: треугольник ABC, A= 27 B= 22 C= 42 Найти: длины его сторон, длины медиан, и cos его углов.

0,0(0 оценок)

Ответ:

Wolf2002

19.03.2023 20:27

треугольнике ABC со сторонами AB=2 см, BC=3 см и AC=3 см проведена биссектриса BM. Найдите длины отрезков AM и MC.

№2 В треугольнике MNKизвестны длины сторон MN=4 см,NK=5 см, NP — биссектриса, а разность длин отрезковMP и PKравна 0,5 см. Найдите MPи PK.

№3 треугольнике DEP проведена биссектрисаEK. Найдите стороныDE и EP,если DK=3 см, KP=4 см, а периметр треугольника DEP равен 21 см.

№4 В треугольнике ABC: BC-AB=3 см, биссектриса BD делит сторону AC на отрезки AD=2 см и DC=3 см. Найдите длины сторон AB и BC

№6 Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, что вершиныM,F и N лежат соответственно на сторонах CD,CE и DE. Найдите стороны CB и DE, если CF=8 см;EF=12 см. В прямоугольном треугольнике проведена биссектриса острого угла. Известно что эта биссектриса делит противолежащий катет на отрезки 4 см и 5 см. Найдите площадь прямоугольного треугольника.

Точка O на гипотенузе равноудалена от двух катетов прямоугольного треугольника и делит

0,0(0 оценок)

Популярные вопросы: Геометрия