1) неверно, поскольку у остроугольного треугольника все 3 угла острые
2) Да, существует, поскольку сумма углов треугольника составляет 180°. 170+9+1=180°
3) Не может, потому что в прямоугольном треугольнике 2 катета и одна гипотенуза
4) Нет не может, потому что в этом случае два угла должны быть равны при основании и тогда их сумма составит 90+90=180°, без учёта третьего угла, а сумма всех 3-х углов треугольника составляет 180°, в нашем случае сумма углов получится более 180°
5) Да, если внутренний угол треугольника 30°, тогда внешний угол составит 180–30=150°
6) Нет, поскольку если внешний угол равен 50°, тогда внутренний угол будет равен 180–50=130°. В прямоугольном треугольнике не может быть тупого угла, потому что один угол прямой=90°, а 2 других - острые - менее 90°
7) Нет, не может быть угол 100° в прямоугольном треугольнике, потому что один угол 90°, а остальные острые - меньше 90°
8) Нет, не существует поскольку сумма острых углов прямоугольного треугольника равна 90°, не более.
Если все грани пирамиды находятся под одинаковым углом к основанию, значит вершина S пирамиды должна быть равноудалена от всех сторон основания пирамиды=> проекция точки S, точка O также должна быть равноудалена от всех сторон пирамиды, значит она находится в точке пересечения биссектрис углов треугольника который лежит в основании.
Допустим AB=BC=32 дм, тогда из точки B опустим высоту/биссектрису/медиану BH на основание AC, так как O∈BH и BH⊥AC=> по теореме о трех перпендикуляров SH будет ⊥ AC.
Угол OHS двугранный=45° по условию.
--------
Треугольник SOH прямоугольный т.к. SO⊥плоскости(ABC)=>SO⊥OH.
так-же он равнобедренный так-как ∠OSH=180-90-45=45=∠SHO, значит высота SO=OH.
Задача свелась к простейшей планиметрической задаче по нахождению OH.
Объяснение:
1) неверно, поскольку у остроугольного треугольника все 3 угла острые
2) Да, существует, поскольку сумма углов треугольника составляет 180°. 170+9+1=180°
3) Не может, потому что в прямоугольном треугольнике 2 катета и одна гипотенуза
4) Нет не может, потому что в этом случае два угла должны быть равны при основании и тогда их сумма составит 90+90=180°, без учёта третьего угла, а сумма всех 3-х углов треугольника составляет 180°, в нашем случае сумма углов получится более 180°
5) Да, если внутренний угол треугольника 30°, тогда внешний угол составит 180–30=150°
6) Нет, поскольку если внешний угол равен 50°, тогда внутренний угол будет равен 180–50=130°. В прямоугольном треугольнике не может быть тупого угла, потому что один угол прямой=90°, а 2 других - острые - менее 90°
7) Нет, не может быть угол 100° в прямоугольном треугольнике, потому что один угол 90°, а остальные острые - меньше 90°
8) Нет, не существует поскольку сумма острых углов прямоугольного треугольника равна 90°, не более.
Если все грани пирамиды находятся под одинаковым углом к основанию, значит вершина S пирамиды должна быть равноудалена от всех сторон основания пирамиды=> проекция точки S, точка O также должна быть равноудалена от всех сторон пирамиды, значит она находится в точке пересечения биссектрис углов треугольника который лежит в основании.
Допустим AB=BC=32 дм, тогда из точки B опустим высоту/биссектрису/медиану BH на основание AC, так как O∈BH и BH⊥AC=> по теореме о трех перпендикуляров SH будет ⊥ AC.
Угол OHS двугранный=45° по условию.
--------
Треугольник SOH прямоугольный т.к. SO⊥плоскости(ABC)=>SO⊥OH.
так-же он равнобедренный так-как ∠OSH=180-90-45=45=∠SHO, значит высота SO=OH.
Задача свелась к простейшей планиметрической задаче по нахождению OH.
---------------------
сделаем вынос Треугольника ABC:
AO биссектриса, BH-медиана/высота.
По теореме пифагора:
Из свойств биссектрисы для треугольника ABH:
ответ: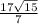
--------------
Если что-то непонятно задай вопрос.