В параллелограмме, тупой угол которого равен 150°, острый равен 180-150=30°
Биссектриса делит тупой угол пополам, следовательно, угол при пересечении ее со стороной, к которой она проведена,тоже равен ее половине ( сумма углов треугольника, так же, как сумма углов параллелограмма при одной стороне, равна 180°).
Благодаря биссектрисе получился равнобедренный треугольник с углами при основании, равными 75° ( это значения здесь не имеет) и сторонами 16 см.
Меньшая сторона параллелограмма равна 16 см, высота, которую мы проведем из вершины тупого угла к большей стороне, равна половине от 16,т.к. противолежит углу 30°.
Имеем все данные для вычисления площади параллелограмма:
высота 8 см
основание 16+5=21 см
S=8·21= 168 см²
-----------------
2..
Площадь треугольника равна половине произведения высоты на основание, к которому она проведена.
Высота h=7√2*sin (45º)=7√2* √2:2=7*2:2=7см Основание =10 см S=19*7:2=35 cм²
-------------------------------------------
Третья задача - в рисунке, ничего сложного там нет - разберетесь.
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
В параллелограмме, тупой угол которого равен 150°, острый равен 180-150=30°
Биссектриса делит тупой угол пополам, следовательно, угол при пересечении ее со стороной, к которой она проведена,тоже равен ее половине ( сумма углов треугольника, так же, как сумма углов параллелограмма при одной стороне, равна 180°).
Благодаря биссектрисе получился равнобедренный треугольник с углами при основании, равными 75° ( это значения здесь не имеет) и сторонами 16 см.
Меньшая сторона параллелограмма равна 16 см, высота, которую мы проведем из вершины тупого угла к большей стороне, равна половине от 16,т.к. противолежит углу 30°.
Имеем все данные для вычисления площади параллелограмма:
высота 8 см
основание 16+5=21 см
S=8·21= 168 см²
-----------------
2..
Площадь треугольника равна половине произведения высоты на основание, к которому она проведена.
Высота
h=7√2*sin (45º)=7√2* √2:2=7*2:2=7см
Основание =10 см
S=19*7:2=35 cм²
-------------------------------------------
Третья задача - в рисунке, ничего сложного там нет - разберетесь.
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство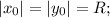
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)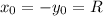 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и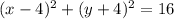
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили