Есть такое свойство в произвольном треугольнике, что точка пересечения серединных перпендикуляров — это центр описанной окружности.
Тоесть, если мы проведём с этого центра отрезок до какой-то вершины треугольника — то этот отрезок будет равен радиусу описанной окружности.
HC == BH == AH = R.
<A = 80°; <AFH == <AEH = 90° ⇒ <FHE = 360-(90+90+80) = 100°.
<FHE = 100° ⇒ <EHC = 180-100 = 80°.
<EHC = 80°; <HEC = 90° ⇒ <HCE = 90-80 = 10°.
AC = 6.
AE == EC = AC/2 ⇒ AE == EC = 6/2 = 3.
EC = 3; <HCE = 10°(α), тоесть — по теореме тангенсов:
Как я говорила, отрезок, проведённый с вершины треугольника до центра описанной окружности — равен радиусу, тоесть:
Вывод: R = 17.26.
6) Проведём сечение АА1СВ через боковое ребро и апофему.
Фигура в сечении трапеция. Пусть её высота равна h. Основания как высоты в равносторонних треугольниках равны:
А1С = 6*(√3/2) = 3√3.
АВ = 12*(√3/2) = 6√3. Разница между ними равна 3√3.
Из свойств правильной треугольной пирамиды известно, что проекция бокового ребра на основание в 2 раза больше проекции апофемы.
Пусть это будут 2х и х.
Получаем 3х = 3√3, отсюда х = √3.
По условию h/x = tg 30°, тогда h = x*tg 30° = √3*(1/√3) = 1.
Отсюда апофема как гипотенуза при катете против угла 30 градусов равна 2х = 2.
Находим площадь боковой поверхности.
Sбок = 3*((6 + 12)/2)*2 = 3*18 = 48.
Площади оснований S = a²√3/4.
S1 = 6²√3/4 = 9√3.
Sо = 12²√3/4 = 36√3.
ответ: S = 48+45√3.
Есть такое свойство в произвольном треугольнике, что точка пересечения серединных перпендикуляров — это центр описанной окружности.
Тоесть, если мы проведём с этого центра отрезок до какой-то вершины треугольника — то этот отрезок будет равен радиусу описанной окружности.
HC == BH == AH = R.
<A = 80°; <AFH == <AEH = 90° ⇒ <FHE = 360-(90+90+80) = 100°.
<FHE = 100° ⇒ <EHC = 180-100 = 80°.
<EHC = 80°; <HEC = 90° ⇒ <HCE = 90-80 = 10°.
AC = 6.
AE == EC = AC/2 ⇒ AE == EC = 6/2 = 3.
EC = 3; <HCE = 10°(α), тоесть — по теореме тангенсов:
Как я говорила, отрезок, проведённый с вершины треугольника до центра описанной окружности — равен радиусу, тоесть: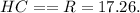
Вывод: R = 17.26.
6) Проведём сечение АА1СВ через боковое ребро и апофему.
Фигура в сечении трапеция. Пусть её высота равна h. Основания как высоты в равносторонних треугольниках равны:
А1С = 6*(√3/2) = 3√3.
АВ = 12*(√3/2) = 6√3. Разница между ними равна 3√3.
Из свойств правильной треугольной пирамиды известно, что проекция бокового ребра на основание в 2 раза больше проекции апофемы.
Пусть это будут 2х и х.
Получаем 3х = 3√3, отсюда х = √3.
По условию h/x = tg 30°, тогда h = x*tg 30° = √3*(1/√3) = 1.
Отсюда апофема как гипотенуза при катете против угла 30 градусов равна 2х = 2.
Находим площадь боковой поверхности.
Sбок = 3*((6 + 12)/2)*2 = 3*18 = 48.
Площади оснований S = a²√3/4.
S1 = 6²√3/4 = 9√3.
Sо = 12²√3/4 = 36√3.
ответ: S = 48+45√3.