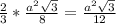ABC – равносторонний треугольник со стороной a. AM и BN – медианы
треугольника, K = AM ∩ BN. Найдите площадь четырёхугольника CMKN.
Объяснение:
S( равност.)=.
S(FBN)=S(CBN), т.к основания равны и высоты из вершины В одинаковые. S(CBN) = .
Проведем СК . S(ВМК)=S(СМК) , т.к основания ВМ=МС , а высота h -одинаковая.
S(СКN)=S(СМК) как площади равных треугольников . Равны по трем сторонам СК-общая , CN=CM ,KN=KM по свойству медиан треугольника.
Значит S(СМКN)=
ABC – равносторонний треугольник со стороной a. AM и BN – медианы
треугольника, K = AM ∩ BN. Найдите площадь четырёхугольника CMKN.
Объяснение:
S( равност.)=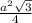 .
.
S(FBN)=S(CBN), т.к основания равны и высоты из вершины В одинаковые. S(CBN) =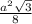 .
.
Проведем СК . S(ВМК)=S(СМК) , т.к основания ВМ=МС , а высота h -одинаковая.
S(СКN)=S(СМК) как площади равных треугольников . Равны по трем сторонам СК-общая , CN=CM ,KN=KM по свойству медиан треугольника.
Значит S(СМКN)=