Abcda1b1c1d1- прямой параллепипед, основанием которого является ромб abcd, dk перпендекулярно a, k э ab, kt паралельно aa1, t э a1b1, докажите, что угол tkd является линейным углом двугранного угла a1abd
Проведены 2 высоту, которые образуют 2 прямых угла.
В четырёхугольнике AC1MB1 — нам известны углы <AC1M; <AB1M.
<C1MB1 — вертикален с углом <BMC — тоесть они друг другу равны, тесть: <C1MB1 = 140°.
Вывод: <A = 40°; <B == <C = 70°.
2.
<BAK = 120° => <BAC = 180-120 = 60° =>
<B = 90-60 = 30°.
Тоерема 30-градусного угла прямоугольного треугольника такова: сторона, противолежащая углу 30-и градусов в прямоугольном треугольнике — равна половине гипотенузы, тоесть: CA = BA/2.
Так как у нас 2 условия с одними и теми же переменными, составим систему:
Объявим стороны как переменные x; y:
AB = 12; AC = 6.
4.
1) Поэкспериментируем: <A == <B = 90°; <C = x
<C = 180-(90+90) = 0.
Сумма всех трёх углов треугольника всегда равняется 180°, если в треугольнике будет 2 прямых угла, то оставшийся третий угол будет равен нулю, тоесть, такой треугольник не может существовать.
2)
Катет, противолежащий углу 30 градусов — равен половине гипотенузы.
3)
Так ка как в прямоугольном треугольнике нам уже известен один угол — прямой угол, то сумма оставшихся двух острых углов равняется 90 градусам. И так как треугольник равнобёдренный, то острые углы равны, что и означает, что каждый из них равен: 90/2 = 45°.
4)
Медиана, проведённая к гипотенузе через прямой угол — равна половине гипотенузы.
ответ:С1С и В1В при пересечении образовали 2 пары вертикальных углОВ
<С1МВ1=<ВМС=140 градусов
<С1МВ=<В1МС=(360-140•2):2=40 градусов
<С1ВМ=<В1СМ=180-(90+40)=50 градусов
Треугольник ВМС
<В=<С=(180-140):2=20 градусов
Треугольник АВС
<В=<С=50+20=70 градусов
<А=180-70•2=40 градусов
Номер 2
Внешний и смежный с ним внутренний угол равны в сумме 180 градусов
<А=180-120=60 градусов
<В=90-60=30 градусов
Треугольник прямоугольный,катет АС лежит против угла 30 градусов,следовательно,он в два раза меньше гипотенузы
АС-х
АВ-2х
х+2х=18
х=18:3
х=6
АС=6 см
АВ=6•2=12 см
Номер 3
Треугольник не может иметь два прямых угла,т к сумма всех углов треугольника равна 180 градусов
Катет,лежащий против угла 30 градусов,вдвое меньше гипотенузы
В равнобедренном прямоугольном треугольнике углы при основании равны по 45 градусов
Медиана,проведённая из вершины прямого угла,равна половине гипотенузы
Объяснение:
1.
Проведены 2 высоту, которые образуют 2 прямых угла.
В четырёхугольнике AC1MB1 — нам известны углы <AC1M; <AB1M.
<C1MB1 — вертикален с углом <BMC — тоесть они друг другу равны, тесть: <C1MB1 = 140°.
Вывод: <A = 40°; <B == <C = 70°.
2.
<BAK = 120° => <BAC = 180-120 = 60° =>
<B = 90-60 = 30°.
Тоерема 30-градусного угла прямоугольного треугольника такова: сторона, противолежащая углу 30-и градусов в прямоугольном треугольнике — равна половине гипотенузы, тоесть: CA = BA/2.
Так как у нас 2 условия с одними и теми же переменными, составим систему: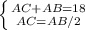
Объявим стороны как переменные x; y:
AB = 12; AC = 6.
4.
1) Поэкспериментируем: <A == <B = 90°; <C = x
<C = 180-(90+90) = 0.
Сумма всех трёх углов треугольника всегда равняется 180°, если в треугольнике будет 2 прямых угла, то оставшийся третий угол будет равен нулю, тоесть, такой треугольник не может существовать.
2)
Катет, противолежащий углу 30 градусов — равен половине гипотенузы.
3)
Так ка как в прямоугольном треугольнике нам уже известен один угол — прямой угол, то сумма оставшихся двух острых углов равняется 90 градусам. И так как треугольник равнобёдренный, то острые углы равны, что и означает, что каждый из них равен: 90/2 = 45°.
4)
Медиана, проведённая к гипотенузе через прямой угол — равна половине гипотенузы.