Касательные имеют теорему: радиус, проведённый с точки касания до центра окружности — перпендикулярен её касательной.
То есть:
Так что, треугольники COB & OAB — прямоугольные.
Нам известна гипотенуза OB, равна 24см, и катет CB — равный 12см.
Что-что!?, что мы замечаем? Гипотенуза OB в 2 раза больше катета CB?
Правильно:
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Теорема действует и в обратном порядке: Если катет равен половине гипотенузы, то ему прилежащий угол равен 30°, что и означает, что:
Теорема о 2 касательных, проведённых с одной точки таков: Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.
Значит OB — биссектриса, что и означает, что <B = 30*2 = 60°.
Касательные имеют теорему: радиус, проведённый с точки касания до центра окружности — перпендикулярен её касательной.
То есть: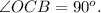
Так что, треугольники COB & OAB — прямоугольные.
Нам известна гипотенуза OB, равна 24см, и катет CB — равный 12см.
Что-что!?, что мы замечаем? Гипотенуза OB в 2 раза больше катета CB?
Правильно: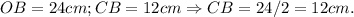
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Теорема действует и в обратном порядке: Если катет равен половине гипотенузы, то ему прилежащий угол равен 30°, что и означает, что:
Теорема о 2 касательных, проведённых с одной точки таков: Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.
Значит OB — биссектриса, что и означает, что <B = 30*2 = 60°.
Вывод: угол между касательными равен 60°.