АВ
АС
8 клас КР No 3 Подібність трикутників
Варіант IV
1. ДKLM ~ДDET, KL: DE = 6: 5. Знайдіть відношення ET: LM.
А. 5:11. Б. 6: 5. В. 6: 11. Г. 5:6
2. Укажіть умови, за яких ДАВС ~ДА, В,С,.
A. ZA = ZA, A + А. Б. ZB = ZB, LA = 32°, 2А, = 28°.
1 А, В, А,С,
в. с- с. Ас - вс г. AB - AC AC + вс
E-1" А, С, В, С, А, В, А,c'A,C, *вса"
3. Дано: MK || PL, OM = 4 см, MP = 6 см, OK = 2 см. Знайти: KL.
А. 3 см. Б. 12 см. В. 5 см. Г. 4 см.
4. Знайдіть катет прямокутного трикутника, проекція якого на
. 07
гіпотенузу дорівнює 1 см, а гіпотенуза - 9 см.
5. BD – бісектриса трикутника ABC, AB = 12 см, ВС = 16 см. Більший з
відрізків, на які бісектриса BD ділить сторону AC, дорівнює 8 см. В.
Знайдіть AC.
6. Знайдіть на малюнку подібні трикутники та доведіть їх
подібність.
Сторони трикутника відносяться як 4:5:7. Знайдіть невідомі
АД
—
сторони подібного йому трикутника, сума більшої і меншої сторін якого
дорівнює 22 см.
Точка о – точка перетину діагоналей трапеції ABCD з основами АВ і СD,
AB = 15 см, DC = 10 см. Знайдіть відрізки D0 iOB, якщо ВD = 20 см.
9. Основи рівнобічної трапеції дорівнюють 16 см і 20 см. Знайдіть висоту
рівнобічної трапеції, якщо її діагональ перпендикулярна до бічної сторони.​

Объяснение: в треугольнике с 30,60,90 есть такое  свойтво наименьший катет А(противолежит углу 30 ) а другой катет    (протеволежит углу 60 )A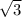 а гипотенуза равна 2A  так вот в 4 задаче так и выходит СD=3,5  AD=7 и AC=3,5 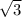 тогда исходя из свойства угол D=60гр так как противолежит AC , так как СB=CD исходя из того что AC общая высота и для ACD и ABC  то треугольник ABC равносторонний и угол В=60     5) тут аналогично используем тоже самое свойство уголs KPC=30 ; PKC=60 ;CKE=30;CEK=60 тогда СE=4,5 так как противолежит  углу в 30гр и   СK=4,5 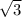; а PC=CK* 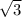= =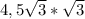13,5   ответ     CE=4,5 PC=13,5                           если вам интересно откуда взялось это свойство то почитайте в интернете свойства треугольника с 30,60,90 градусами

20,6 м

Объяснение:

Объяснение

х - старая длина поля

у - старая ширина поля

Согласно условию задачи составляем первое уравнение системы (по теореме Пифагора) :

х² + у² = 10 000 (сумма квадратов катетов = квадрату гипотенузы)

х - 62  - новая длина поля

у - 50  - новая ширина поля

2х + 2у - старый периметр поля

2(х - 62) + 2(у - 50) новый периметр поля

Согласно условию задачи, новый периметр меньше старого в 5 раз, составляем второе уравнение системы:

2(х - 62) + 2(у - 50) = (2х + 2у) / 5

Умножим обе части уравнения на 5, чтобы избавиться от дробного выражения, получим:

5(2х -224 + 2у) = 2х + 2у

10х + 10у -2х -2у = 1120

8х + 8у = 1120, сократим на 8:

х + у = 140, выразим х через у:

х = 140 -у  и подставим значение х в первое уравнение:

(140 - у)² + у² = 10000, раскрываем скобки, квадрат разности:

19600 - 280у + у² + у² = 10000

2у² -280у + 9600 = 0, сократим на 2:

у² - 140у + 4800 = 0

Получили квадратное уравнение, ищем корни:

у первое, второе = (140 плюс минус √19600-19200) / 2

у первое, второе = (140 плюс минус √400) / 2

у первое, второе = (140 плюс минус  20) / 2

у первое = 60 (ширина), тогда х первое( длина) = 140 - 60 = 80

у второе = 90 (ширина), тогда х первое( длина) = 140 - 90 = 50

Вторую пару х и у отбрасываем, т.к длина не может быть меньше ширины.

Итак, новая длина поля 80 - 62 = 18 (м)

         новая ширина поля 60 - 50 = 10 (м)

Ищем диагональ нового поля: √18² + 10² = √424 ≅ 20,6

Проверка

Старый периметр: 2*80 + 2*60 = 280 (м)

Новый периметр: 2*18 + 2*10 = 56 (м)

280 : 56 = 5 (раз), соответствует условию задачи.