Бічна сторона рівнобічної трапеції дорівнює 10 см, більша з її основ - 17 см, висота - 8 см. Обчисліть периметр трапеції. *​

1) V =32P см кубических Sбок = 32P см квадратных Sобщ  = 36P см квадратных

2) V = 30P см кубических  Sбок = 98.34 см квадратных   Sобщ = 126.6 см квадратных

3) V =  8P см кубических   S = 16P  см квадратных

Объяснение:

1) Sбок = 2PRh

Sбок = 2*8*4/2*P = 32P см квадратных

Sобщ = Sбок + Sосн

Sосн = PR в квадрате

Sосн = 4P см квадратных

Sобщ = 32P+4P = 36P см квадратных

V = Sосн*h

V = 4P*8 = 32P см кубических

2) Sбок = PRL

L = = =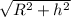

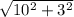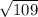
Sбок = 3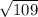P = 98.34 см квадратных

Sосн = PR в квадрате

Sосн = 9P = 28.26 см квадратных

Sобщ = Sбок + Sосн

Sобщ = 98.34 +28.26 =126.6 см квадратных

V = 1/3*P*h*R в квадрате

V = 1/3*P*10*9 = 30P см кубических

3) V = PR в кубе

V = (4/2)в кубе *P = 8P см кубических

S = 4PR в квадрате

S = 16P  см квадратных

1. Найдем отношение ВР к СР;

Через вершину В проводим прямую параллельную  АС.

АР продлеваем за точку Р до пересечения с прямой в точке Е. 

=> ВЕ параллельно AC; 

Треугольники ЕВК и АКМ подобны, следовательно:

ЕВ относится к АМ как ВК относится к КМ;

2)  ВК/КМ=1, и ЕВ=АМ; ( треугольники равны). 

Отсюда следует:  ЕВ = АС/2; 

Треугольники ЕВР и АСР подобны

=> ВР/СР = ЕВ/АС = 1/2;

итак СР = ВС*2/3; и, соответственно, площадь треугольника АСР

S ACP= S*2/3; (S - площадь треугольника АВС).

т.к S треугольника ВАМ=1/2 S АВС,

а S АКМ=1/2 S АВМ, то 

S AKM = S/4;

Таким образом, площадь четырехугольника КРСМ равна

S KPCM = S ACP - S AKM = S*(2/3 - 1/4) = S*5/12;

ответ 12/5;