Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а)
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
в) Найти площадь боковой поверхности - самая простая часть этого задания:
, где и - периметр основания и высота пераллелепипеда соответственно.
Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а)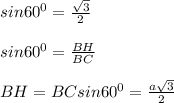
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
в) Найти площадь боковой поверхности - самая простая часть этого задания:
г)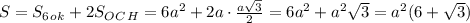
Отрезок BD - диаметр окружности с центром О. Хорда AC делит
пополам радиус OB и перпендикулярна к нему. Найдите углы
четырёхугольника ABCD и градусные меры дуг AB BC CD и AD.
Соединим центр окружности с вершиной А.
Отрезок ОА - радиус, МО равен его половине.
sin ∠ МАО равен МО: АО=1/2.
Это синус 30°∠ МАО=30°, ⇒∠ АОВ=60°.
ВО=АО=радиус окружности. ⇒ △ АОВ равнобедренный.
Сумма углов треугольника 180 градусов.
∠ ОВА=∠ОАВ=(180°-60°):2)=60° ⇒ △ АОВ- равносторонний.
Углы ВАD и ВСD опираются на диаметр ⇒ они прямые=90°.
⊿ ВСD и ⊿ВАD -прямоугольные, и
∠СDВ=∠АDВ=180°-(90°-60°)=30°
⊿ ВСD=⊿ВАD.
∠ D=2 ·∠АDВ=2·30°=60°
Сумма углов четырехугольника 360°
∠АВС=360°- 2·90°- 60°=120°
Градусная мера дуги равна центральному углу, который на нее
опирается.
На дугу АВ опирается центральный угол АОВ=60°⇒ ее градусная мера 60°
На дугу СВ опирается центральный угол СОВ=60°⇒ ее градусная мера 60°
В треугольнике САD ∠САD=∠DАС=60°
Вписанный угол равен половине градусной меры дуги, на которую
опирается.
На дугу CD опирается вписанный угол САD=60°⇒ она равна 2·60°=120°
На дугу АD опирается вписанный угол АСD=60°⇒ она равна 2·60°=120°
∠А=С=90°
∠В=120°
∠Д=60°
градусные меры дуг
AB=60°
BC=60°
CD=120°
AD=120°.