Обозначим ∠А = α.
∠СВА = 90° - α (сумма острых углов прямоугольного треугольника равна 90°)
Тогда в прямоугольном треугольнике ВСН:
∠ВСН = 90° - ∠СВА = 90° - (90° - α) = α
Точка М симметрична точке В относительно точки Н, значит
СВ = СМ, Δ ВСМ - равнобедренный, тогда его высота СН является биссектрисой:
∠МСН = ∠ВСН = α
∠ОСК = ∠ВСА - (∠МСН + ∠ВСН) = 90° - (α + α) = 90° - 2α
АК = ВК по условию, значит ΔАВК равнобедренный,
∠КАВ = ∠КВА = α
∠СКВ = 2α как внешний для ΔАКВ (внешний угол треугольника равен сумме двух внутренних, не смежных с ним)
Если назвать угол иначе, то ∠СКО = 2α.
В треугольнике ОСК:
∠ОСК + ∠СКО = 90° - 2α + 2α = 90°, тогда
∠СОК = 90°, следовательно
ВК⊥СМ.
Разложите вектора а,b,с по координатным векторам i , j
Объяснение:
Любой вектор на плоскости можно представить в виде суммы или разности векторов.
Если вектор а можно представить в виде ,где х,у числа , то координаты вектора
1) Вектор а равен сумме 2-х векторов j, тк направления совпадают , длина вектора а в 2 раза больше : , (0:2).
2)По клеточкам нарисуем треугольник , так чтобы вектор b был стороной этого треугольника. Выразим вектор b по правилу треугольника : сектор b=АВ+ВС.
Но ⇒ , координаты b(-2;-2).
3)Вектор с равен вектору -i , тк направления не совпадают , длина вектора c равна длине вектора i : , (-1:0).
Обозначим ∠А = α.
∠СВА = 90° - α (сумма острых углов прямоугольного треугольника равна 90°)
Тогда в прямоугольном треугольнике ВСН:
∠ВСН = 90° - ∠СВА = 90° - (90° - α) = α
Точка М симметрична точке В относительно точки Н, значит
СВ = СМ, Δ ВСМ - равнобедренный, тогда его высота СН является биссектрисой:
∠МСН = ∠ВСН = α
∠ОСК = ∠ВСА - (∠МСН + ∠ВСН) = 90° - (α + α) = 90° - 2α
АК = ВК по условию, значит ΔАВК равнобедренный,
∠КАВ = ∠КВА = α
∠СКВ = 2α как внешний для ΔАКВ (внешний угол треугольника равен сумме двух внутренних, не смежных с ним)
Если назвать угол иначе, то ∠СКО = 2α.
В треугольнике ОСК:
∠ОСК + ∠СКО = 90° - 2α + 2α = 90°, тогда
∠СОК = 90°, следовательно
ВК⊥СМ.
Разложите вектора а,b,с по координатным векторам i , j
Объяснение:
Любой вектор на плоскости можно представить в виде суммы или разности векторов.
Если вектор а можно представить в виде
,где х,у числа , то координаты вектора 
1) Вектор а равен сумме 2-х векторов j, тк направления совпадают , длина вектора а в 2 раза больше :
, 
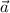(0:2).
2)По клеточкам нарисуем треугольник , так чтобы вектор b был стороной этого треугольника. Выразим вектор b по правилу треугольника : сектор b=АВ+ВС.
Но
⇒ 
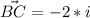, координаты b(-2;-2).
3)Вектор с равен вектору -i , тк направления не совпадают , длина вектора c равна длине вектора i :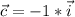
, 
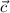(-1:0).