БИЛЕТ No 15 1.Сформулируйте и докажите теорему, выражающую первый признак равенства треугольников. 2. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? 3. Объясните, как с циркуля построить биссектрису данного угла. 4. По данным рисунка докажите, что треугольник ВДР равнобедренный В 5. Начертите утол ABC равный 150. С циркуля и линейки разделите его на 4 равных утла.
Объяснение:
Дано: отрезок АВ, прямая а, а⊥АВ, АО=ОВ. Доказать что АС=ВС.
Возьмем на прямой а точку С, построим ΔАВС.
АО=ОВ, ∠АОС=∠ВОС=90° по условию, СО - общая сторона, значит
ΔАОС=ΔВОС и тогда АС=ВС. Доказано.
4.
Дано:
ABC - прямоугольный треугольник
AB = 5см
BC = 12см
AC - гипотенуза
BD - высота, опущенная на гипотенузу AC
Для начала вычислим длину гипотенузы AC, воспользовавшись теоремой Пифагора:
Опустив высоту AD на гипотенузу AC у нас получилось два прямоугольный треугольника - ABD с гипотенузой AB и BCD с гипотенузой BC. Пусть AD = x, тогда DC = 13 - x, так как AC = 13 см.
Поскольку высота AD является общим катетом для треугольников ABD и BCD запишем:
Итак, AD = x =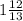 см., а DC = 13 - x =
см., а DC = 13 - x = 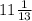 см.
см.
Найдём высоту BD:
Высота BD делит гипотенузу AC на отрезки 1 12/13 см. и 11 1/13 см.
Высота BD равна 4,615 см.
(странные какие-то цифры, но я перепроверил решение несколько раз - всё сходится вроде бы...)
5.
Косинус угла равен отношению прилежащего катета к гипотенузе.
AB является гипотенузой. Следовательно:
cos(30) = 2 / AB